第1回はこちら:ソーティング
第3回はこちら:探索アルゴリズム
あいさつ
こんにちは、Syncorです。連載だしルビはいいかなと思って省略しました。
さて、アルゴリズムを学びなおすSyncor第2回です。第1回を書き始めたときはこの第2回の内容をどうしようか悩んでいたんですが、第1回を書き終えた後に「まだ色々書いた方がいいかもなこれ…」となったのでこのタイトルになりました。
前回同様、ゆる~くやっていきます。よろしくお願いいたします。
ヒープソートについて
さてさて、第2回を始めましょう。第1回の時はソーティングアルゴリズム、その中でも「バブルソート」「クイックソート」「マージソート」の3つを取り上げました。この記事シリーズは自分の勉強も兼ねてというかほぼそれがメインで書いているので、ChatGPTだけでなくあっちこっち色んなサイトを見て調べて回っていたんですが、そこかしこで「ヒープソート」というものを目にしたんです。
私専門が情報科学とかではなく、もろもろ独学でやっているのですが、お恥ずかしながらこれ知らなかったんですね。ただ結構使えそうというか、なんかこう、良い感じな気がしたので取り扱おうと思います。我ながら語彙力ないですね。
概要
前回はある程度は知っていたものを取り扱ったのでさらさら書いてましたが、今回は勉強しながら書くので、なおのこと間違ってたりごちゃごちゃしてたりすると思いますがお許しください。
さてまずヒープソートについて。ヒープソートとは、配列とかの整理するデータを「ヒープ」の性質をもった木構造の形に並べて整理していくアルゴリズム...ですかね。
そして「ヒープ」とは、「親≦子」or「子≦親」の関係を持つように整理された二分木のことです。言葉だけで書くとちょっとわかりづらいですね。実際に配列を用意して、整理を進めてみながら確認してみましょうか。
実際にやってみる(木の整理編)

さて、まずこのように配列を用意してみました。ではこれを二分木の形でまとめてみましょう。
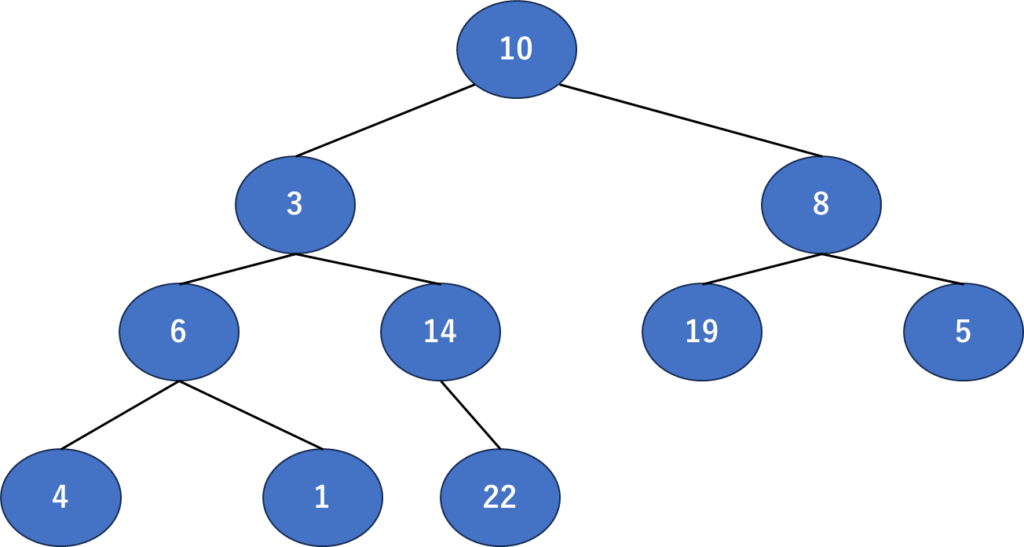
こんな感じですかね。概要でちょっと書いた「親」が二分するところの元?でいいんでしょうか。10とかは明らかに親ですね。
さて、とりあえず書いてみましたが、まだ並べただけです。これをヒープになるように並び替えてみましょう。
先ほど、ヒープとは「「親≦子」or「子≦親」の関係を持つように整理された二分木のこと」と説明しましたね。今回は「子≦親」となるように整理してみましょう。
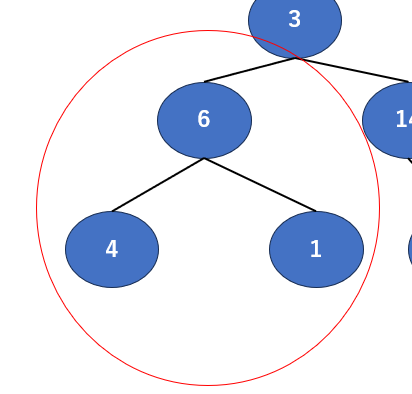
まずはここに注目しましょう。この部分二分木とでも言うのでしょうか、ここでの「親」は6で、「子」が4と1ですね。これに対して、今回定めたルールである「子≦親」が成り立っているか確認します。
確認すると、今回は6が一番大きいので、「子≦親」が成り立っていることがわかりますね。なので今回はこのままにします。
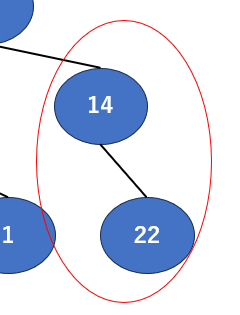
では次にここを確認しましょう。ここでの「親」は14、「子」は22ですね。同様に比較してみると…子の方が大きいですね。これでは「子≦親」に反してしまいます。
今回はここを入れ替えます。今回は1本だけなので単純に変えるだけですが、親が一番大きくなるように入れ替えます。
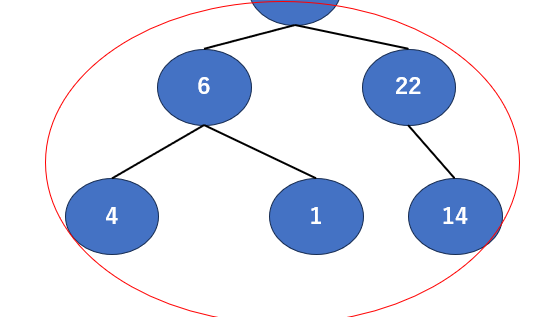
入れ替えてみました。変化がわかりやすいように最初のものも合わせて撮ってます。
さて、階層を1つ上にして次の段階に行きましょう。
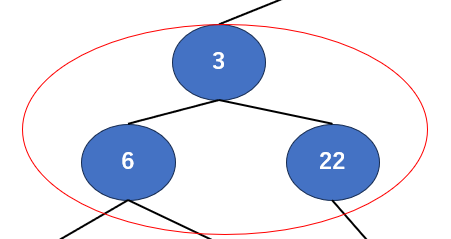
今度は2分木になりましたね。親と子がどれになるか…慣れてきましたかね?
次は「親」が3,「子」が6と22ですね。先ほど親だった6・22が子になりました。
さぁ比較しましょう。あれこれ議論するまでもなく子の22が一番大きいですね。では入れ替えましょう。
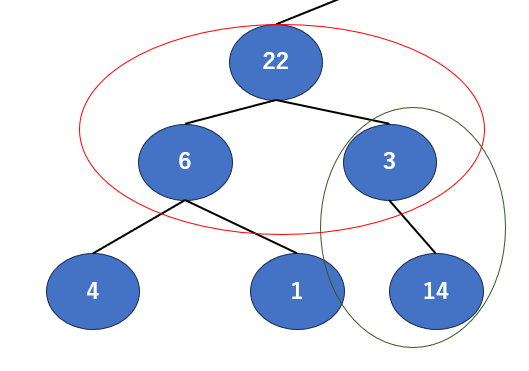
さて入れ替わって親が22になりました。では次のエリアに…行く前にちょっと待った!1個確認しなきゃいけないことがあります。
今回の入れ替えで右にあった22が3と入れ替わりました。しかし先ほどの22は14と比べて大きいことがわかったうえで配置されたものです。しかし3と入れ替わってしまったため、その保証ができなくなってしまっています。なので再度確認が必要になります。
では緑のエリアに注目しましょう。親が3,子が14…おや、親の方が小さくなってしまいました。チェックしておいてよかったですね。ではここを再度入れ替えておきましょう。
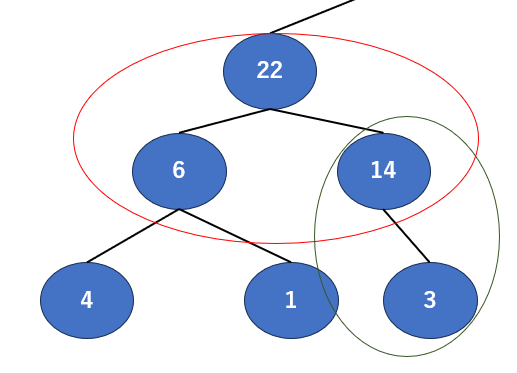
さて、こうなりました。これでどの部分に注目しても「子≦親」の関係性が成り立っているはずです。安心して次のエリアに行きましょう。
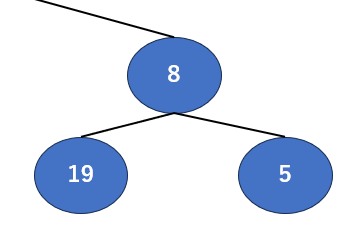
さて次のエリアです。省略してもいい気がしますが、僕自身がそれで苦しんだ過去があるので確認も兼ねてちゃんと書いてみましょう。
今回は「親」が8,「子」が19と5ですね。比較すると…今回は子の19が一番大きそうです。では19と親の8を入れ替えましょう。
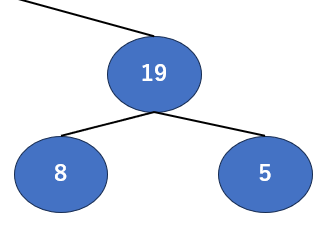
こうなりました。もう慣れてきましたかね?
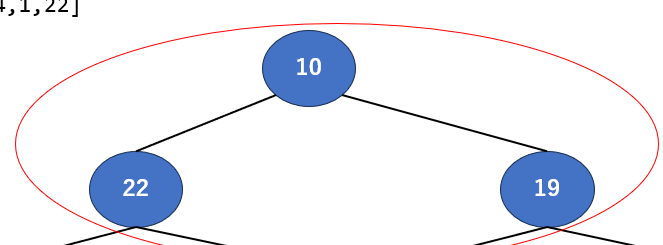
さて、一番上に来ました。でもサクッと行きましょう。今回は親が10で子が22,19ですね。一番大きいのは22なので入れ替えます。
さて入れ替えが終わ…りじゃないですね。22と10を入れ替えたので、左側の保証が無くなりました。というわけでまだまだ行きましょう。
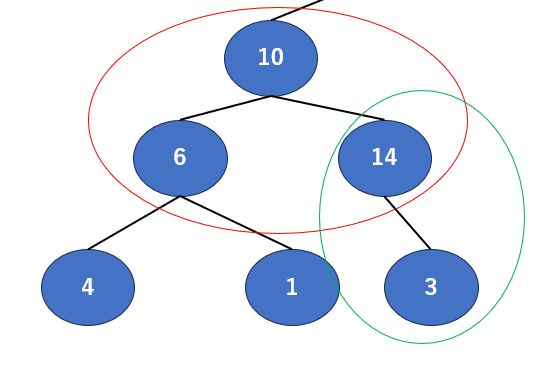
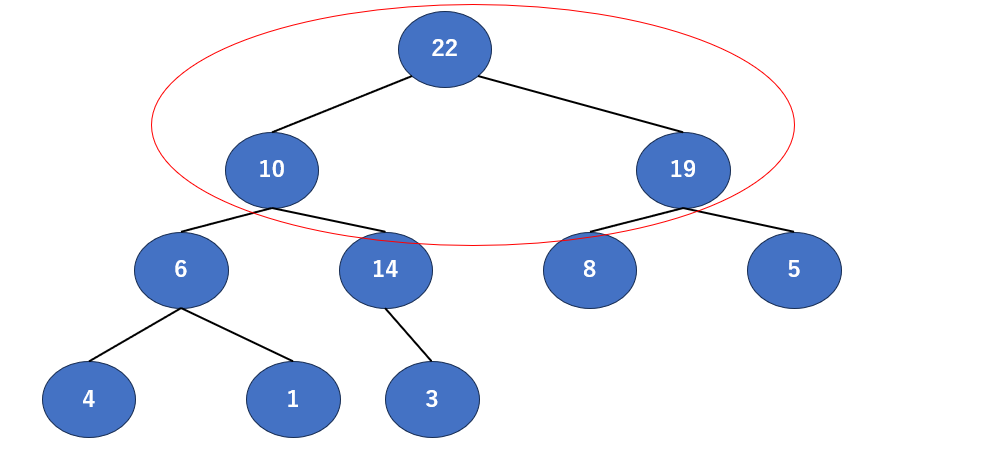
さて、ここですね。そろそろ多少省いても許されますかね?
まずは赤エリア、ここを見ると…親の10より子の14の方が大きいです。入れ替えましょう。
そして入れ替えると14側の保証が無くなるので、緑エリアのチェックが必要です。変わると親が10,子が3になりますね。ですが幸いにも、ここは親の方が大きいので入れ替える必要はなさそうです。助かりました。
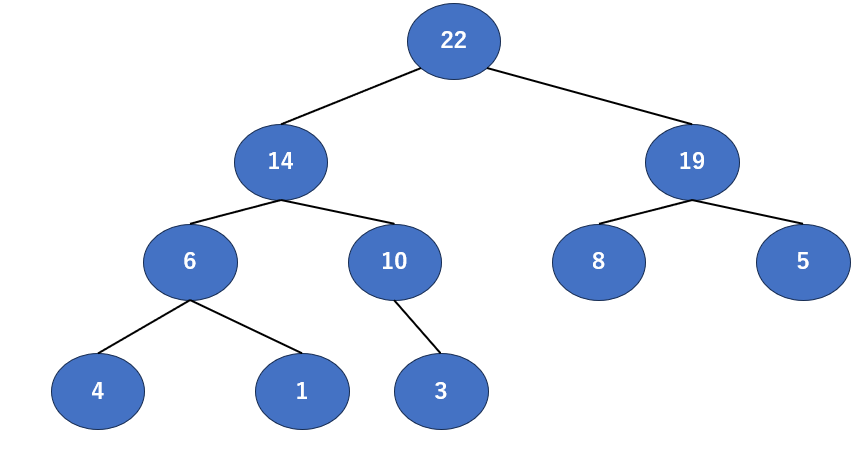
こうなりました~なんかだいぶ疲れた気がしますね。ですがまだ並べ終わっただけです。これを回収していかなきゃいけません。
実際にやってみる(回収編)
タイトルこれでいいのだろうか…まぁいいや
整理編で作った木の要素を回収していきましょう。さっき作ったやつを再掲します。
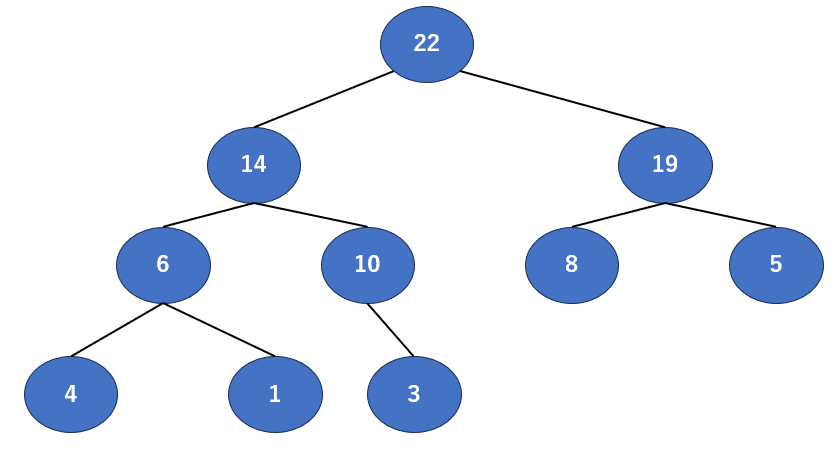
この木のどこから回収するかというと、一番上の親、「根(ルート)」の部分です。
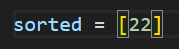
回収すると..根が消えます。困りました。木が瓦解しちゃいますね。なので代わりに最下層にあった4を持ってくることにしましょう。
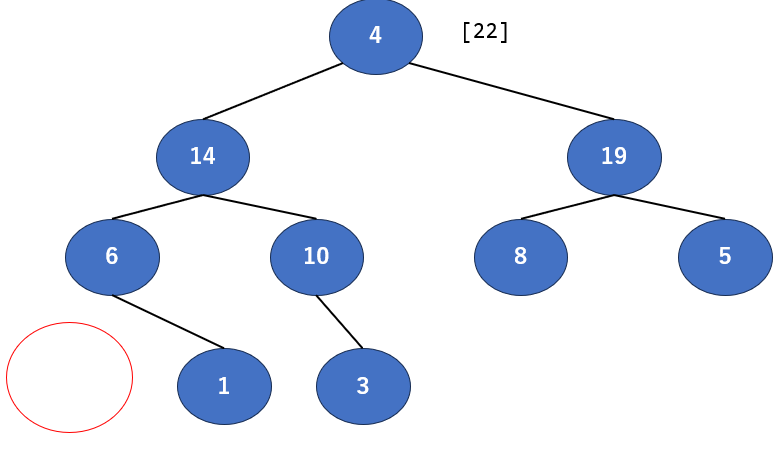
さて、これで木が更新されたのでよ…くはありませんね。先ほどまでずっとやってきたように、木が更新されると保証が消えます。なので、同じようにもう1度整理しましょう。では一番上を確認します。
最上層を確認すると、親が4,子が14、19で子の19が明らかに一番大きいですね。では更新しましょう。
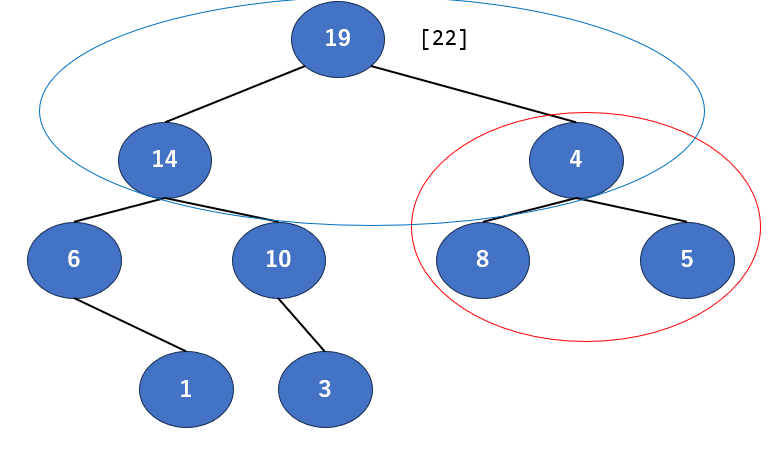
さて、間違えてなければこうなると思います。右の19と親の4が入れ替わりました。
…もう大丈夫ですかね?そうです。次は右側の保証が無くなりました。では今度は赤いエリアをチェックしましょう。
今回は親が4、子が8と5ですね。ということは子の8と親の4を入れ替えることになりそうです。早速行きましょう。
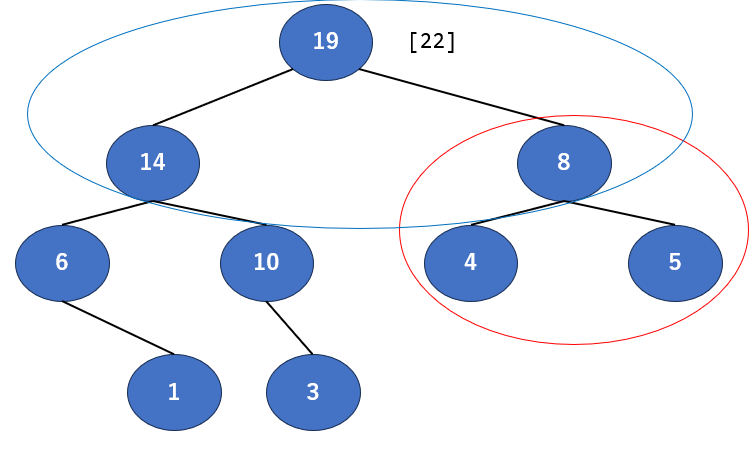
できました。ぱっと見また整理できてそうですね。ではまた回収しましょう。次の根は19ですね。また根が消えちゃうので1を上に持っていきます。
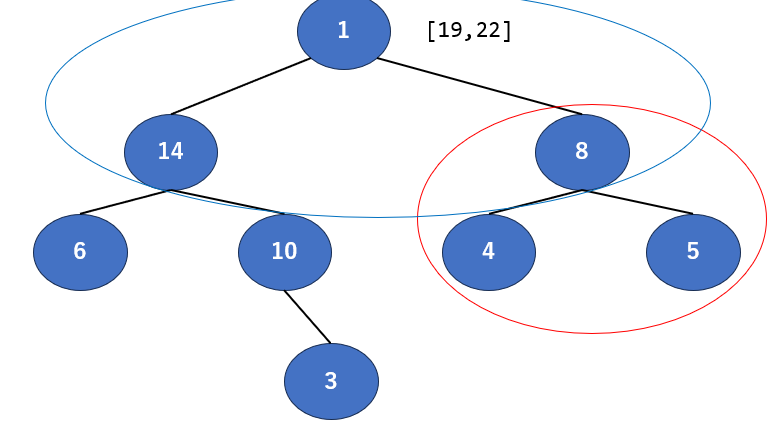
さて、こうなりました。おや、木が更新されたということは…というように、整理⇒回収⇒移動⇒整理⇒回収…とやっていき、最終的に全要素を拾いきるように進めていきます。
これがヒープソート、だそうです。いろいろ調べながら書いてみましたが合ってますかね?間違ってたら悲しみに打ちひしがれておくことにします。
後々の手順は割愛します。とんでもなく長くなりそうですし。
いやぁ~にしても大変なアルゴリズムですね。何に使うんだこれ…という問いの答えは実は薄々感づいてる…つもりです。間違ってたら恥ずかしいですね。これについては次の計算量の項目で話すことにしましょう。
サンプルコード(Made by ChatGPT)と解釈
さて、サンプルコードを出してみましょう。まぁ自分で0から書いても良かったんですが、時間かかる自信しかないのとある技術は使おうの精神でGPT君にお願いします。アルゴリズムの理解の方が本質だしね。じゃあGPT君よろしく~

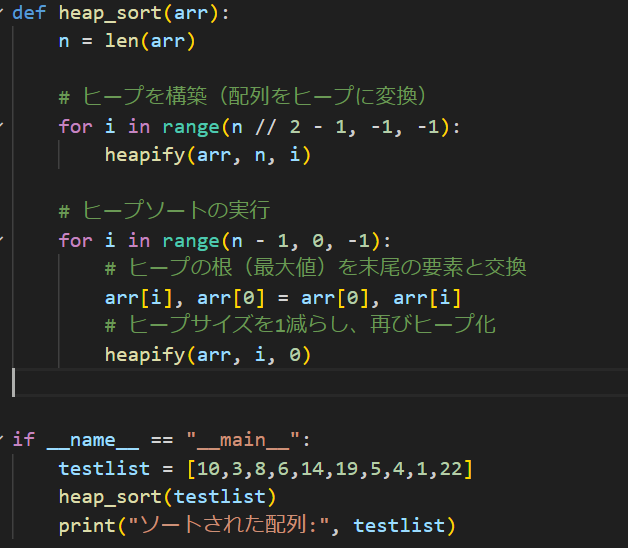
お願いしたらこんな感じになりました。

ふぅ。GPT君に頼むと時々変なコード出してデバッグが結局大変~ってなったりするんですが今回はすんなりでした。指示がシンプルだとぱっと出てくれていいですね。
さて、前回挙げたアルゴリズムは比較的シンプルだったのでぱっと見で済ませてましたが、今回は複雑ですね。(だからGPTにお願いしたんですけど…)というわけで今回は細かく解釈しましょう。
まず、最初の二分木(並べただけ)に番号を振ってみました。すると
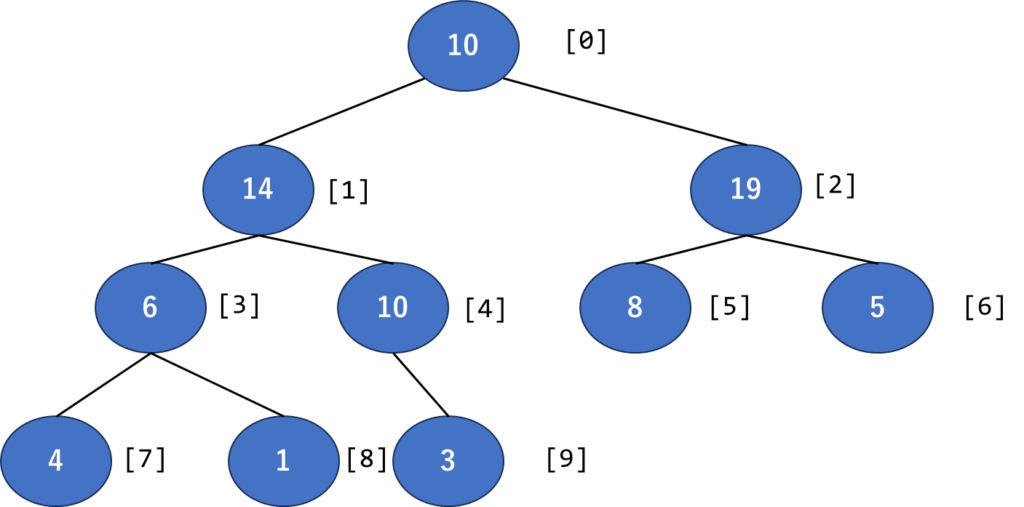
こうなりますね。ここで、各部分二分木に注目すると、親の番号をiとしたとき、子の番号が〈2i+1〉〈2i+2〉となっていることがわかりますね。これで配列内の何番がどれにあたるのかを区別することができそうです。

そしてここ、ここが入れ替えと再チェックの部分で、再帰呼び出しによって実装してるようです。
さて、最後にあと1か所確認しましょう。というかここ以外は割とそのままです。
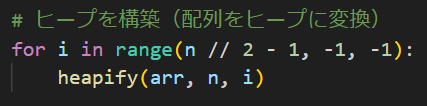
このfor文、rangeの中が少しごちゃっと書いてありますが、なんで(n // 2 – 1, -1, -1)なのか説明できますか?特にn//2-1のとこですね。ここ結構大事です。(nは配列の長さです)
…え?僕ですか?わかんなかったですよ?
なので、GPTと問答して頭の中で計算して確認してきました。その話をします。
まず結論から言うと、n // 2 が最初の葉ノード(子ノードを持たないノード、親になり得ないやつ。)を指します。この計算式で出せるんです。つまりn // 2 -1は最下層の親ノードを指します。
鍵は子ノードの計算式、〈2i+1〉〈2i+2〉にありました。まず当然ですが、子ノードを計算したとき、その結果は配列の長さnを超えることはないはずですよね?もしそうなったら無いものを指すことになります。
逆に言うと、〈2i+1〉〈2i+2〉がnを超えてしまうとき(i≦n)それは葉ノードになるというわけです。
では実際にn//2を代入します。すると…n+1、n+2になってしまいますね。そう。nを超えてしまうわけです。
なので、n // 2は最初の葉ノードになります。ここが境目になっていて、n // 2 ~ n – 1までは葉ノードだということが計算できるわけで、つまりn // 2- 1は親ノードであることが明らかになります。こういう計算だったんですね~
ヒープソートまとめ
なんだかすごく書きすぎてしまった気がします。当初はここまで書く気なかったのに…
この後の計算量の話はざっくりとまとめることにします。尺使いすぎました。
ヒープソートについてご理解いただけましたでしょうか。我ながら結構頑張ったんですがその分間違いが無いか心配です。
このソーティングアルゴリズム、複雑なだけでは…?と思わせながらちゃんと利点が大きそうです。ではその話をするために計算量の話に移りましょう。
計算量
はじめに
先に言います。ざっくりと書きます。あんまり詳しく言うのは避けます。
理由はまずあくまで「概要の理解」が本題だったのもありますがなにより、ヒープソートについてで尺使いすぎました。長すぎても見る気失せるだけだと思いますし。とはいえ大事な内容ではありますのでまた機会があったらちゃんと書こうと思います。はい。誰か書いてくれてもいいけどな~チラチラ
さて、計算量を話すうえで「時間計算量」と「空間計算量」の2種があることは触れなきゃいけません。これもざっくりとだけにしますので、詳しく知りたい方は別途調べてみてください。ちゃんとした説明がきっとあるはずです。あとビッグオー記法ないしランダウの記号については…省略!ごめん!わかんない人は調べるか雰囲気で悟って下さい!わかんない人でもなんとなしにわかるように努力します…
時間計算量
時間計算量とは、まぁその名の通りで「計算にかかる時間」を表します。この時間計算量が大きいと、まぁ例えばプログラムを実行してから終了するまでにすごい時間がかかってしまいます。明確に嫌ですね。
時間計算量が多いアルゴリズムのイメージが一番大きいのがバブルソート。たしかO(n^2)だったと思うんですが、バブルソートをサイズが1000とか10000の配列を対象にやってみるとわかります。すげぇかかる。
対してヒープソートはO(nlogn)です。まぁ要はO(n^2)より高速です。これは実際にやってて、構造上大規模データに対して適応しやすそうだなぁと感じてました。気になる方は巨大データで試してみてください。バブルに比べてかなり早いと思います。
空間計算量
人によってはあまりピンと来ないかもしれません。空間計算量です。
空間計算量の「空間」ってなんぞや?って方いると思うんですが、メモリです。メモリ領域のことを指します。
メモリも使う量が少ないに越したことはありません。パソコンでゲームや動画編集やる方はわかるかもしれませんが、メモリ不足ってのは結構ヤバいです。できるだけメモリ消費が少ない方がありがたいんです。
空間計算量が大きいのは…クイックソートでしょうか。クイックソートはピボットとの大小であるサイズの配列が増えていくので、占有するメモリが増えていきそうです。ちょっと自信ないですが、空間計算量はO(logn)とかだったと思います。気になる方は調べてね。
さて、これに対してヒープソートはめっちゃ少なく済みます。計算量オーダーは本当に自信ないので省きますが、ソースコードを思い出してみましょう。
…新しい配列、生成しましたっけ?
そう、実はヒープソートはずっと配列の中の順番を入れ替える操作しかやっていません。なので最初に用意するデータ分のメモリ以外に用意する必要がほぼないと言えるんですね。個人的にこれが一番大きいメリットで、ここまで複雑な理由かなと感じました。
C、C++みたいなメモリを気にする必要が十二分にある言語だと非常に助かりそうです。ヒープソートすごーい!
終わりに
いかがでしたでしょうか。
え~…
書きすぎました!
マジでここまで長くする予定なかったです。ちょっとヒープソートの説明に熱を入れすぎました。その分計算量トークが雑になった感が全く否めません。本当に申し訳ないです。
まぁ計算量について語りだすと結構しゃべれそうな気がしますし、後々のためのネタ残しということで…今回は雑にしか書いてないのであんまり信用せず、他のサイト等確認してくれると幸いです。僕は責任取れませんので悪しからず。
次回は…探索アルゴリズムについて書く予定です。が、変わるかもわかりません。体力と文量と相談しながらそれっぽいのを書こうと思います。
それでは、Syncorでした。またね~