第1回はこちら:ソーティング
第2回はこちら:ヒープソートと計算量
あいさつ
こんにちは、Syncorです。最近マジで寒くなりましたね。色んな意味で春が待ち遠しいです。
さて、第3回です。ちょっと期間空いちゃってすいません。
今回は「探索アルゴリズム」と題して、いくつかの探索アルゴリズムアルゴリズムに触れていきたいと思います。とはいっても、線形探索とか二分探索ではなくて、木構造とかグラフ構造で使われる深さ優先とかに触れていこうと思います。前者の方期待してた人ごめんね。個人的にソーティングアルゴリズムと同じかそれ以上に大事なものだと思ってます。
一応この3回目で短期集中連載は終わろうと思いますが、なんか書き足らなくなったら第4回が生えるかもしれません。ただ、この3回目で書き足りるように、うまくまとまるよう頑張ってみようと思います。それでは始まります。対戦よろしくお願いします。
探索アルゴリズム
さて、探索アルゴリズムとは!…まぁ探索するアルゴリズムですね。詳細は省きます。線形探索とか、二分探索とかが有名どころかなぁと思うんですが、あいさつでも書いた通り、今回は省きます。
じゃあ何を書くのかといいますと、BFSとDFS、つまり幅優先探索と深さ優先探索について書こうと思います。理由は…まぁゲーム制作で使うことが多いように感じるのでってことです。(線形探索とかは本当に分量の問題で割愛するだけです)
DFS書き終わった時点での文量でどの程度触れるか考えますが、ダイクストラ法とかも触れようかなと思います。それでは対戦よろしくお願いします。
幅優先探索(BFS)
さて、幅優先探索(Breadth-First Search)です。まぁこういったアルゴリズムはグラフ対象ですし、説明する際にあった方がいいと思うのでとりあえず準備しましょう。
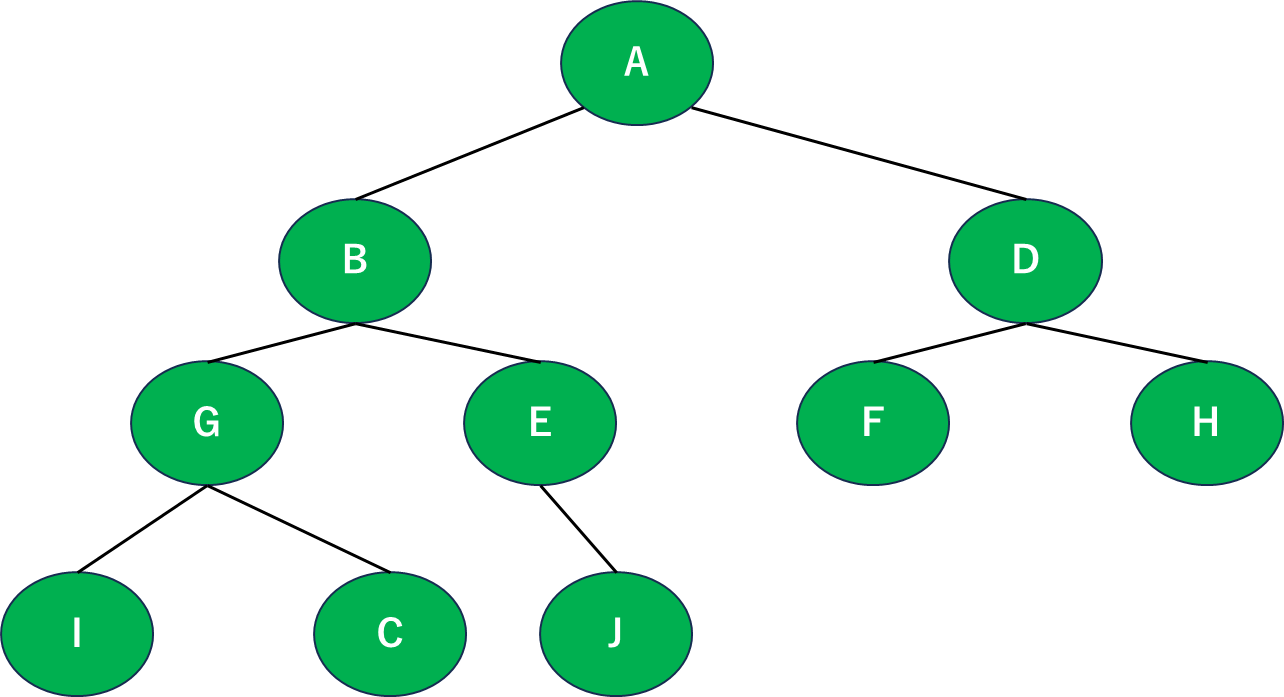
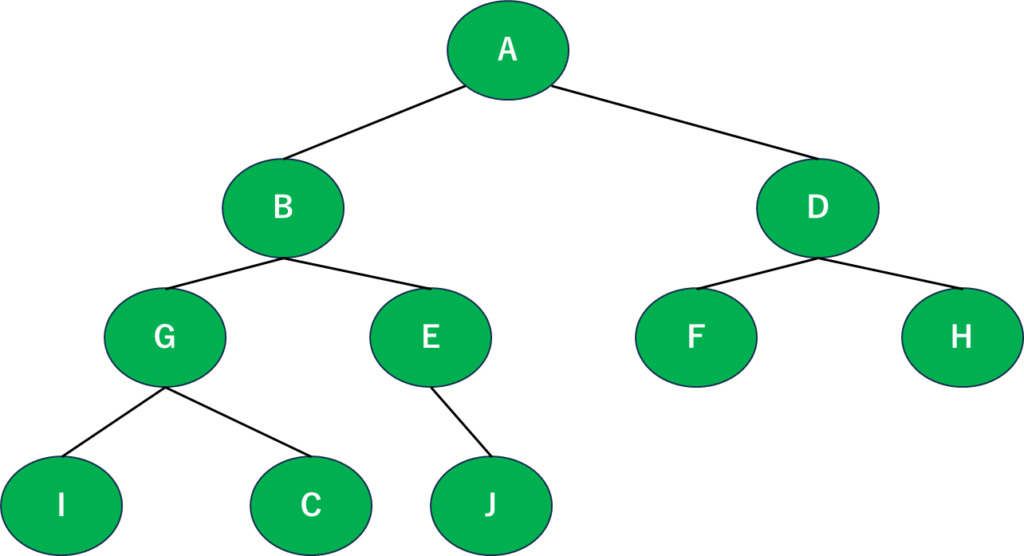
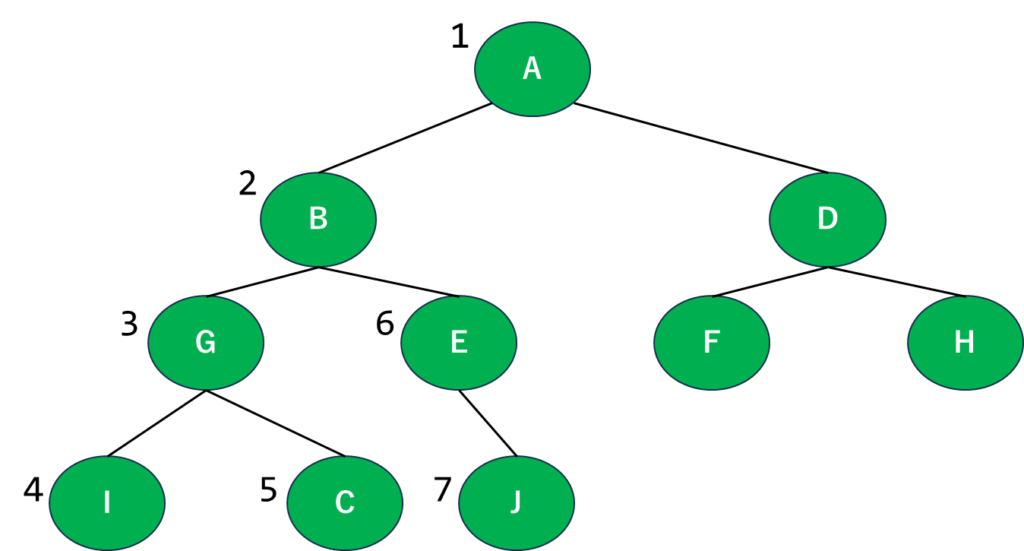
さて、二分木を用意してみました。これを使って考えてみましょう。
探索アルゴリズムなんでなんかを探しに行くアルゴリズムではあるんですが、幅優先探索やこの後書く深さ優先探索も「どう探索していくか」に注目していきたいと思います。
というわけで、とりあえずAをスタートということにしましょう。ここから始めていきます。
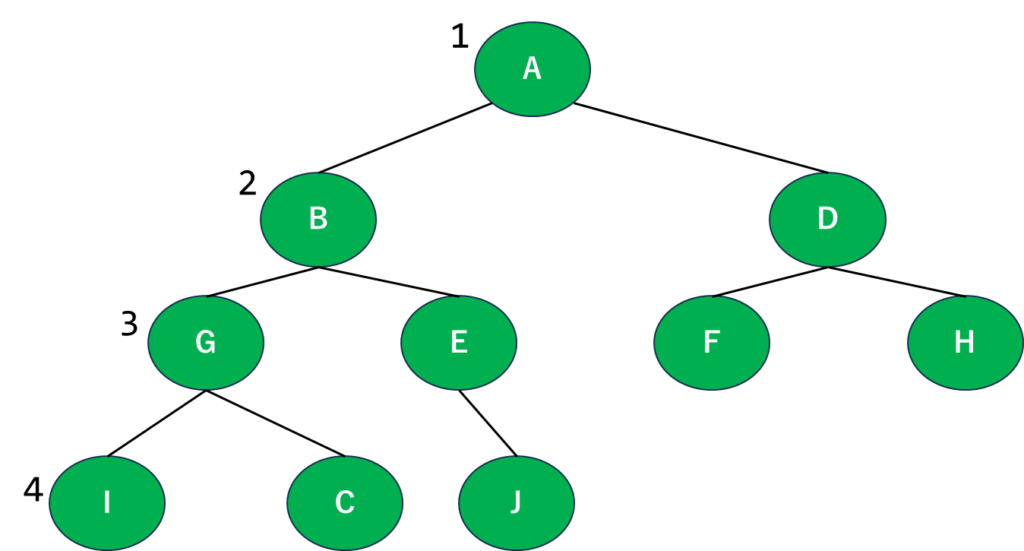
幅優先探索とは、このスタート地点から近い場所から順に探索していくアルゴリズムです。実際に図に番号振ってみましょう。
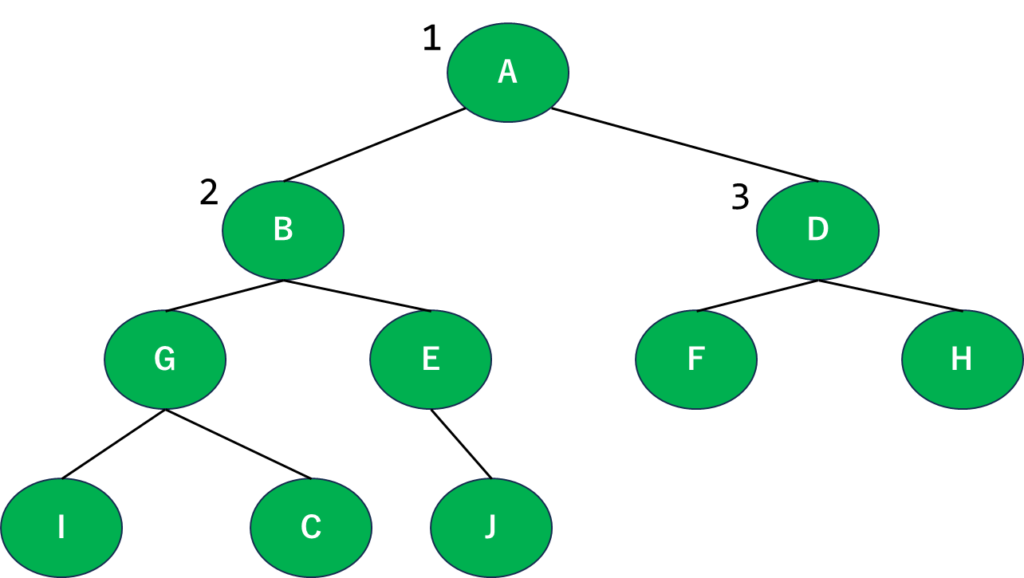
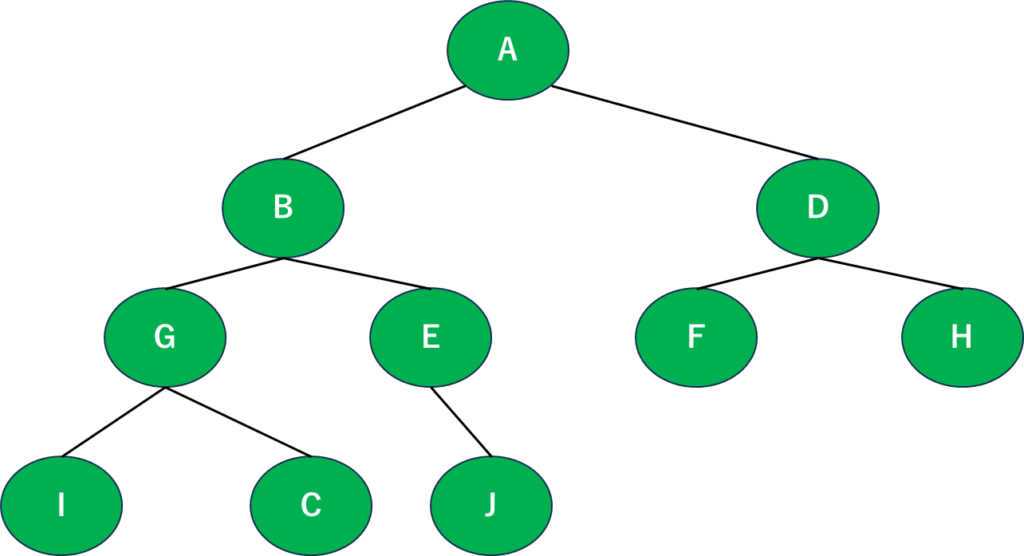
とりあえず1段階分書いてみました。このグラフを見るとスタートのAに一番近い…というか接続してるのがBとDなので、ここが1段階目の探索範囲になりますね。文字に表すとA⇒B⇒Dの順になります。
2段階目に入りましょう。次に注目するのはBとD、順番的にB⇒Dになります。グラフを見ればぱっと見でわかると思いますが、Bから最も近いのがGとE、Dから最も近いのがFとHなので…
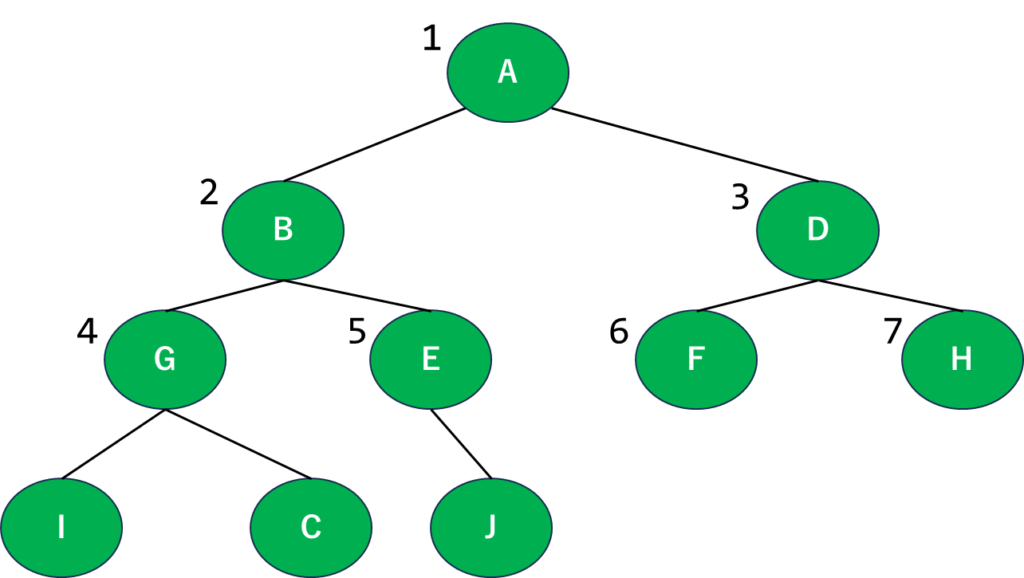
こうなりますね。次の段階もついでにやっちゃいましょう。
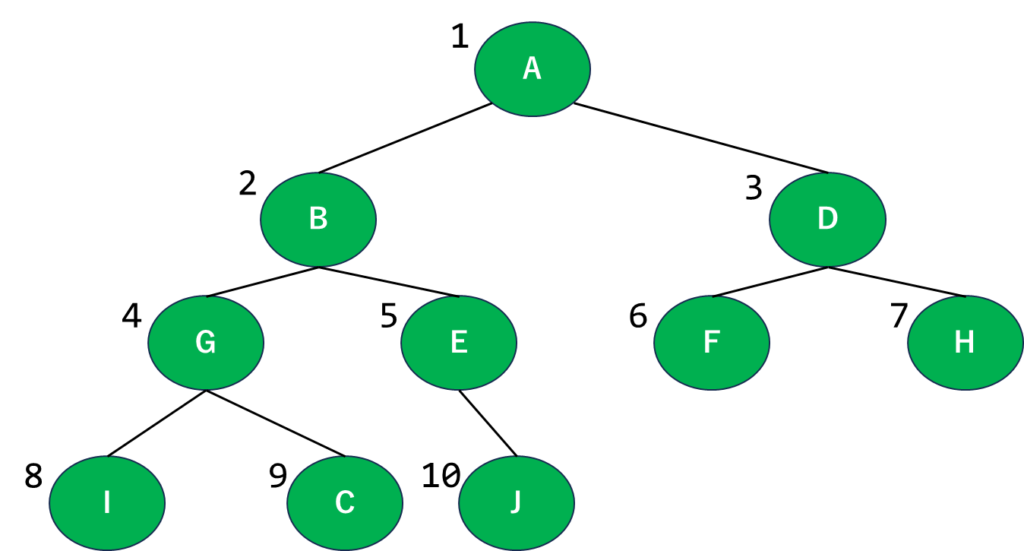
…合ってるよね?こうなると思います。
このように、文字通り「幅」を優先して進んでいくわけです。こうして図にして考えるとすごいシンプルですね。
では概要の話はこのあたりにして、実装・プログラムの部分について話していきましょう。なんとなくこっちの方が長くなる気がします。
実装編:キュー
急に泣き出したわけじゃないです。倒れてもないです。ダジャレでもないです。キュー(Que)です。
スタックと一緒に語られることが多いやつですね。スタックは後程お話しします。
キューというのはデータ構造の一つ…という説明でいいんでしょうかね。FIFO、つまり最初に入れたデータを(First-In)最初に取り出す(First-Out)構造になっております。
まぁ色々言葉で書くより、コードがあった方がわかりやすいと思うので、毎度のごとくGPT君に生成してもらいましょう。
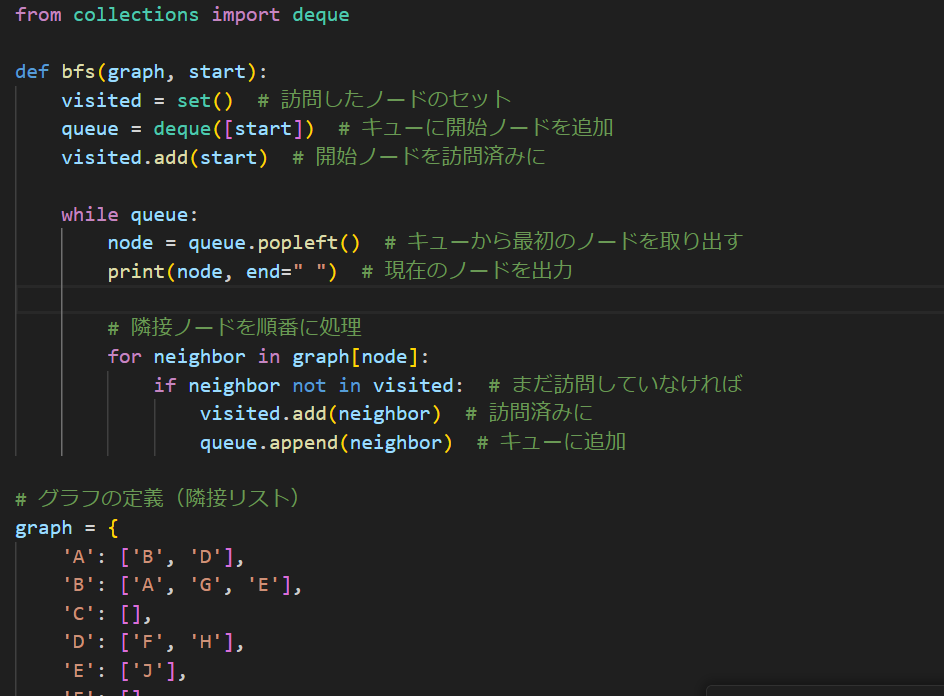
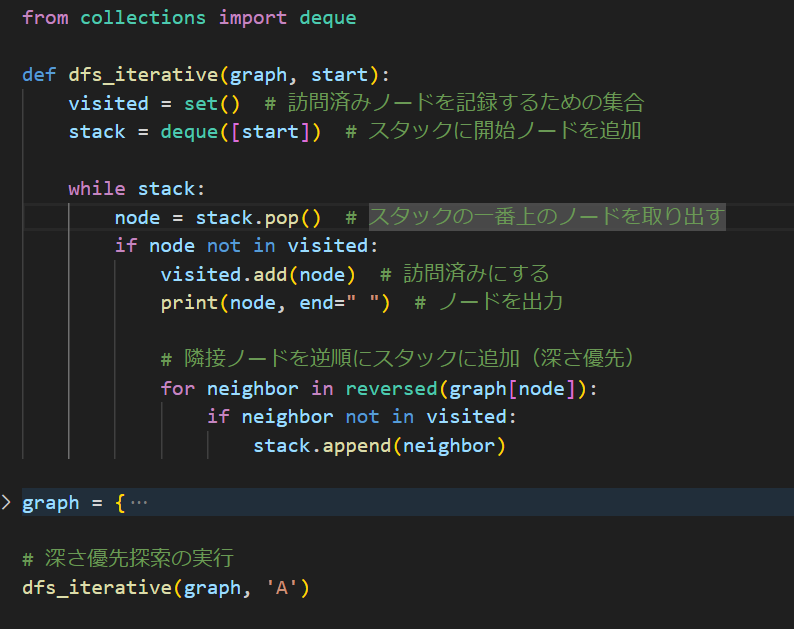
こうなりました。関数BFSを作って、それを下で呼び出してます。それで隣接リストを使って、最初に作ったグラフを表しています。隣接リストに関してはまぁ…省略します。これ話すとまたすごい文章量になりそうなので…
さて、実際のプログラムを見ながら説明を進めていきましょう。ちなみに1行目でdequeというものをimportしていますが、これがque(キュー)と後ほど説明するスタックを実装するのにも使います。

setはまぁなんか集合だと思えば問題ないと思います。startはまぁ引数ですね、mainで以下のように呼ばれてます。
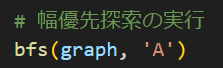
deque([start])で、開始ノードとしてstartで受け取ったもの、今回は”A”ですね。それを追加してキューを準備します。そして、巡回した部分を管理するリストとして”visited”を用意して、さっそくスタートノードを追加しています。ここから探索を始めていきましょう。

さて、whileループの中の序盤のところを持ってきました。おおよそは説明不要だと思いますが、この”queue.popleft”ですね、ここがある意味肝だと思います。
popleft()メソッドはレフトからpop、つまり配列の先頭(キューの中の最初のノード)を取り出してきています。配列は基本左詰めだということを考えれば結構イメージしやすいですかね?
そして、現在のノード(取り出したノード)をprintで出力してます。
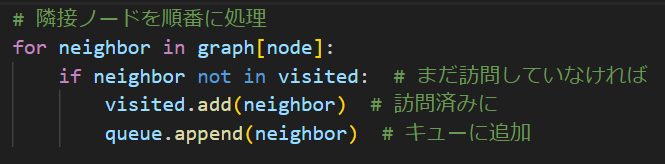
さて、先ほどの部分の続きです。pythonでforeach的な処理書きやすいの好きです。
まずgraph(最初に用意したグラフ)から隣接部分を取り出します。最初に”A”がスタートで呼ばれてたので、今回は隣接してるのが”B”と”D”ですね。これをneighborに取り出します。neighbor、つまり近所・近傍・隣接、まぁそんな意味ですね。
ここで、先ほど準備してたvisitedリストに取り出したneighborが入ってないか確認します。もし入っていた場合は既に見た(訪問した)場所なのでスキップする必要があるわけです。
そしてまだ訪問していない場所であれば、訪問済みリストに追加したうえで、キューに追加します。append()で配列の右側(=末尾)に追加して、逆に左側(=先頭)に追加したい場合はappendleft()を呼び出します。名前がそのままで助かります。
そうしてそれぞれのneighborを見た後、whileの最初に戻ります。でまた先頭を取り出して表示するという流れになっています。
こんな感じでキューの構造としては、データを追加していって、「先に追加したものから先にデータを抜いていく」のでFIFO(First-In First-Out)と呼ばれています。これを使うことで幅優先探索探索を実装しているわけです。
一応キューの構図を図で作ってみましたが…逆にわかりにくいかなこれ…
混乱しそうだったら無視してください。はい。
深さ優先探索(DFS)
深さ優先探索(Depth-First Search)です。幅優先探索の説明の後であれば、なんとなくどういった探索をするのかピンとくるのではないでしょうか。
というわけで、幅優先探索の説明に使った画像と同じものを用いて説明していきましょう。その方が比較しやすいと思いますしね。
では早速始めていきましょう。深さ優先探索とはその名の通り、幅優先探索と違って「深さ」を優先して探索していくアルゴリズムです。そのままですね。幅優先探索では幅を優先して現在の探索位置の幅次元(今回は横)を全部探索してから次の段階に進んでいましたが、深さ優先探索では幅ではなく、深さ次元を全部探索してから次の段階に進みます。
それじゃあ具体的に、”A”をスタートとしましょう。あ、一応今回は行きがけ順でやります。他にも帰りがけ順とかあるらしいんですが、ちゃんと説明できる自信ないのでこの段階で明言しておきます。
とりあえずAからBに向かいましょう。
さて、じゃあ次はどこ行こうかとなるんですが、今回は深さ優先なのでそのまま深さ方向(今回は下)に掘り進めていきます。なので、A⇒Bと来たら、B⇒G⇒Iと行くわけです。
さて、深さを求めて掘り進んで最下層の”I”までたどり着きました。でも未探索のノードはまだまだあります。次はどこを見ましょうか…
現在地は最下層の”I”で親ノード以外に接続しているノードがありません。じゃあその親ノードまで戻ってみましょう。
すると”G”に移動するわけですが、接続ノードを調べると、おやおやまだ調べてないノード”C”が見つかりました。じゃあここに移動しましょう。
では”C”にたどり着きましたが、またもや接続している子ノードがありません。だったら同じように親ノードまで戻りましょう。しかし改めて見ると、ノード”G”も未探索の子ノードがもうありません。
じゃあさらに親のノードを見ましょう。すると、今度は未探索の子ノード”E”が見つかりました。
では”E”に移動しましょう。Eの接続を確認すると…お!今回は未探索の子ノードがさらにあります。ならばそっちも調査しましょう。というわけで、ノード”J”に移動します。
さて、こんな感じになっていると思います。このように進んでいくのが深さ優先探索になります。
さて、Eまで来ました。これで親ノードB以下のノードは探索したので、戻って戻って、Aの子ノードの”D”に進みます。
そして、さっき左優先で行ったのでそこからF⇒Hと。

こう!(のはず)ですね!全部行けたやったー!
こんな感じで、DFSはまさに「深さ」を優先して探索していくアルゴリズムだったわけです。今回は縦向きの二分木を使って説明したのでなんとなくわかったかなと思ってます。横向きのグラフも当然あるわけなので、深さを優先してみるべきか、幅を優先してみるべきかはその場合その場合で見分けが必要ですねうんうん。
間違ってたら結構恥ずかしいですが、ともかく実装編に行きましょう。
実装編:スタック
詰まったわけではないです。むしろ積みます。
幅優先探索を説明した際に、実装で使うため「キュー」の概念もまとめて説明したんですが、今回は「スタック」というものを使います。スタック使わなくても再帰呼び出しを使えば実装できるんですが、スタックの確認も込めてスタック使う方でやります。
では同様に先にコードを生成してもらいましょう。実際のコードがあった方が説明しやすいです。
こうなりました。GPT君にスタックで実装してね!!って言った結果です。普通にお願いしたらどっちも出してくれてました。
ちなみにdeque使わなくても実装できることに気づいたんですが、逆にdequeでも大丈夫だったのでこのまま書きます。もしかしたら後日直すかも
さて、さっそくコードを見ていきましょう。関数始まって最初の2行はあんま説明要らないかなと思いますが、訪問済みリストと使うスタックを生成してます。詳しくはドキュメントとか確認してみてください。

while文の中身を取り出してきました。
…まぁほぼほぼ全体像ですね。stackが空になったら終了する条件でループを開始して、ループ内1行目でpop()で要素を取り出してきています。
今回は最初1個しか要素ないので変わらないのですが、pop()はリストの一番後ろから取り出してきています。幅優先探索のときはpopleft()で前から取り出していたのですが今回は逆ですね。
ここからスタックの性質を使っているのですが、この先の追加する部分も含めて説明したいので先行きましょう。

取り出したnodeが訪問済みじゃない(visitedリストにない)場合は、まずそのノードをvisitedリストに格納します。そして、ノードでの処理(今回は現在のノードの表示)が終わったら、取ってきたノードの隣接部分をスタックに追加していきます。
スタックに追加していくんですが、今回はreversed、つまり逆順に隣接ノードを追加していきます。(グラフは隣接リストで作ってます)
今回使っているグラフは左⇒右の順で優先度をつけているんですが、今回使うスタックは後ろから取り出すため、普通にappendすると、取り出すときに右にあるノードから取り出してしまいます。それを防ぐために逆順で追加処理を行っているわけです。
そして隣接ノード(neighbor)を全部見たら上に戻ってまた次のノードを確認しに行きます。
こんな感じで、最後に追加したもの(Last-In)を最初に取り出す(First-Out)構造になっているのでLIFOと呼ばれています。
…ちなみにですが幅優先探索のことをFIFOと言いますが自分途中までその概念を間違えていて、ここ書いた時点で書き直しに行ってました。多分治ってると思いますが…みなさんは間違えないようしっかり整理してくださいね。
図も毎度のごとくわかりづらかったら無視してください。はい。
探索アルゴリズム(長さ付きグラフ編)
さて、BFSとDFSの説明が無事終わりました。
これで終わろうかなぁとも考えたんですが、やっぱもうちょっと頑張ろうと思います。第4回に続く~ってしたらまた後回しにしそうなので…
なにを話すかというと、先ほどまで上げたグラフは幅・深さの概念を使ってましたが、今度は長さだとか距離と言われる概念を追加したいと思います。まぁようはAからBに行くのに4、AからDに行くのに1かかる~みたいなそんな話ですね。
それを使って何をするかというと、ダイクストラ法と、A*アルゴリズムという2つを勉強したいと思います。いわゆる最短経路探索のアルゴリズムですね。
ただ、BFS・DFS等と違ってマジでうっすらとしか覚えてないので、かなりごちゃごちゃすると思います。丁寧に確認してはいるつもりですが、間違ってたら申し訳ないです。
では早速れっつらご
ダイクストラ法
まずはダイクストラ法から始めていこうと思います。「なんか名前は知ってるな…」って人はそこそこいるのではないでしょうか。僕はまさにそれです。ダイクストラさんが考案されたのでこの名前になったらしいです。
ではまず、距離付きのグラフを準備しましょう。
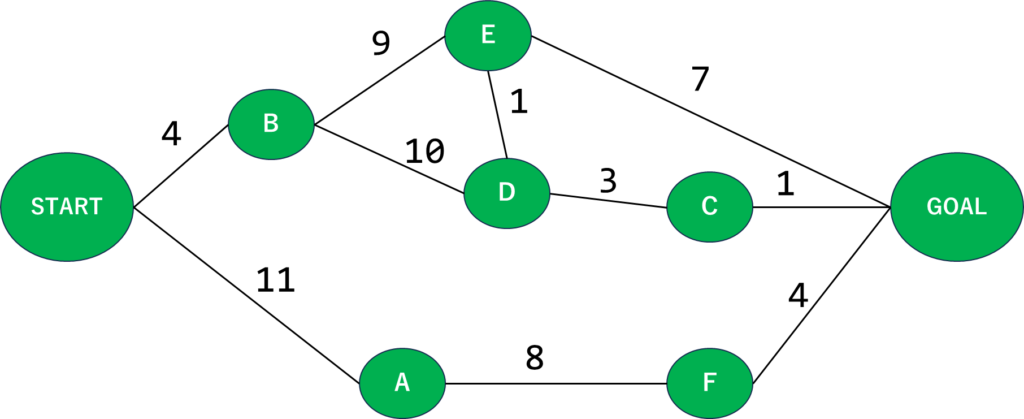
こんなものを用意してみました。最初はSTARTにいると仮定して、ここからGOALまで向かうとすると色んな経路の選択肢があると思うんですが、わざわざ遠回りする理由もないですしやっぱり最短経路で行きたいわけです。
…まぁこのくらいであれば暗算でできそうですが、やっぱりプログラムに計算させて楽をしましょう。こういった場合に最短経路を探索するのに使うアルゴリズムの1つがダイクストラ法になります。
さて、では肝心のアルゴリズムの内容に触れていきましょう。ちょっと色々なサイトを参考にしながら書いていくのでこの時点で定義しておきますが、各ノード(StartとかAとかBとか)を頂点、途中の道を辺と言ったりします。統一するよう意識はしますが、混ざってたらそう認識してください。
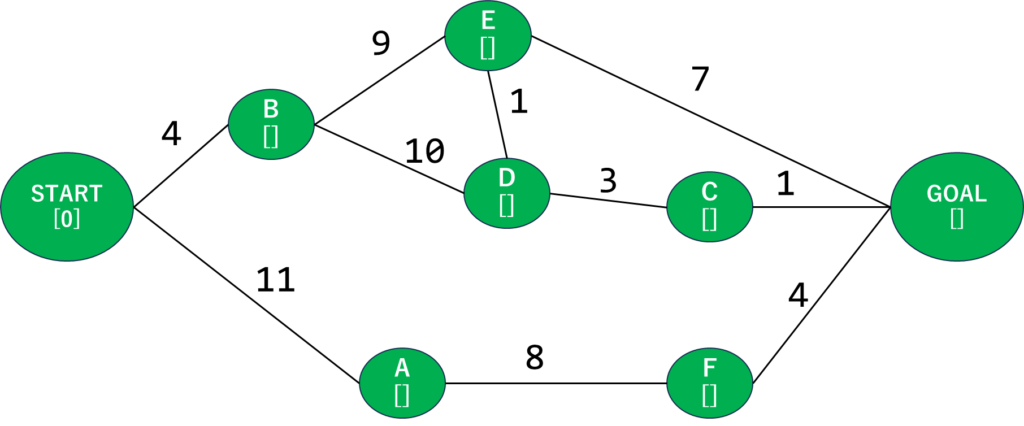
さて、最初に作ったグラフにいくつか要素を追加しました。AとかBの下の[]はそこにたどり着くまでの最短距離が入っています。Startはどう頑張っても0から増えるはずないので0をそのまま入れてます。
まずSTARTから始めます。隣接してる頂点を探すと、AとBが接続していることがわかりますね。そしてそこまでの距離を確認します。STARTからA・Bまでは一本道なので、それぞれにそこまでの距離を設定します。
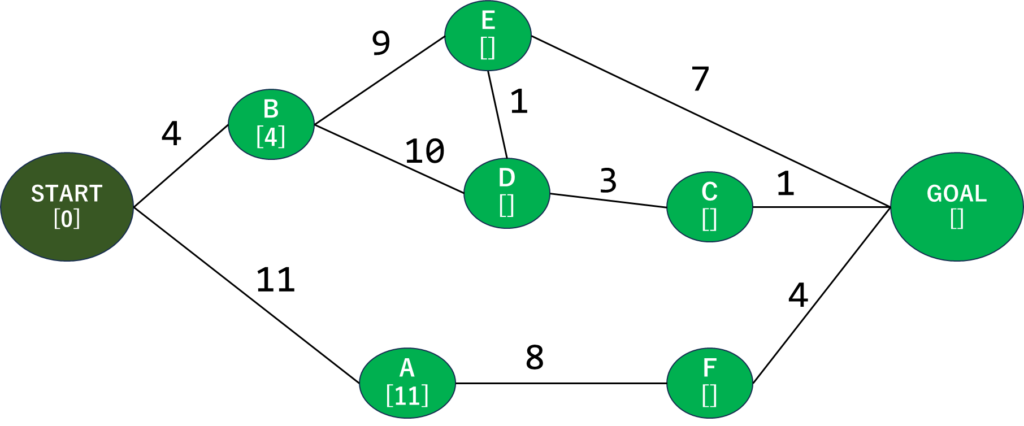
こうなります。ちなみに探索が終了したところ(最短経路が確定+移動済み)は濃い緑にしております。そして、[]の中にそこまでの最短距離を格納しています。
ではどこから行こう…となるんですが、今回のアルゴリズムでは現在の最短距離の場所に移動します。それを踏まえて現在のグラフを見ると…次はBっぽいですね。Bに行きましょう。
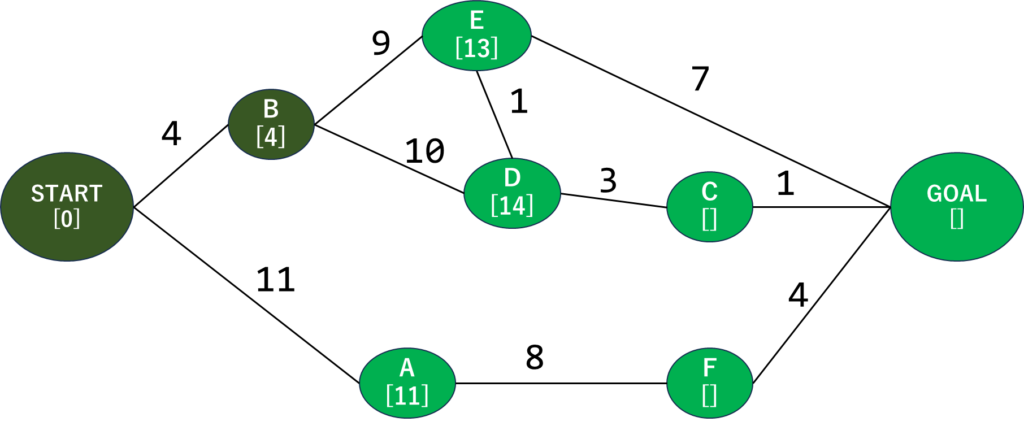
Bに来ました。STARTノードでやったように、隣接してる頂点までの最短距離を計算します。Bに隣接している未探索の頂点を確認すると、EとDですね。BからEまでの距離は9なのでEの[]には9…ではなく、ここに入れるのはSTARTからそこに来るまでの最短距離です。なのでEには、START⇒Bの距離4とB⇒Eの距離9を合計した13が入ります。
同様にDも計算するとSTART⇒Bの4とB⇒Dの10を足して14になりますね。こんな感じで各ノードまでの最短距離を更新します。
では次の探索位置に行きましょう。隣接してるとこに行きたい気持ちがありますがグラフを俯瞰すると…距離11のAが一番短そうですね。あちらから行きましょう。
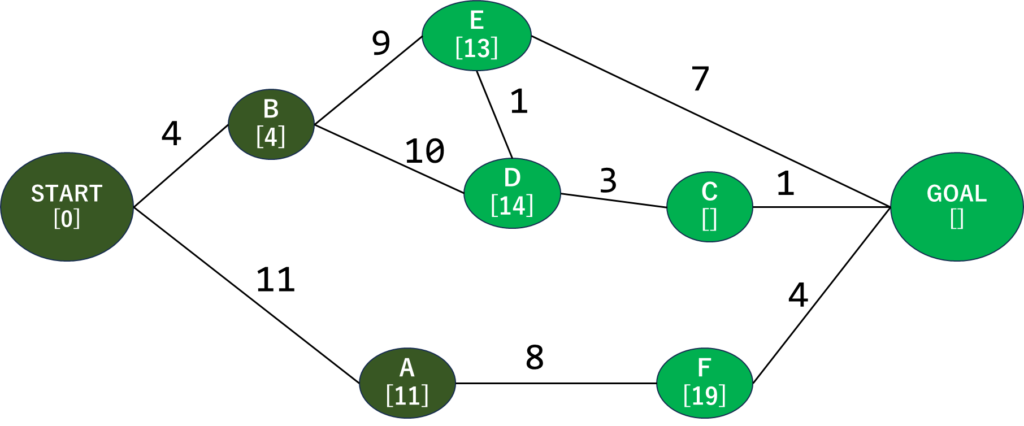
Aに隣接している未探索の頂点を確認すると、Fだけですね。START⇒Aの距離11と、A⇒Fの距離8を足して19が入力されます。
どんどん探索を進めていきましょう。グラフを見ると次に近そうなのは…距離13のEですね。Eに移動します。
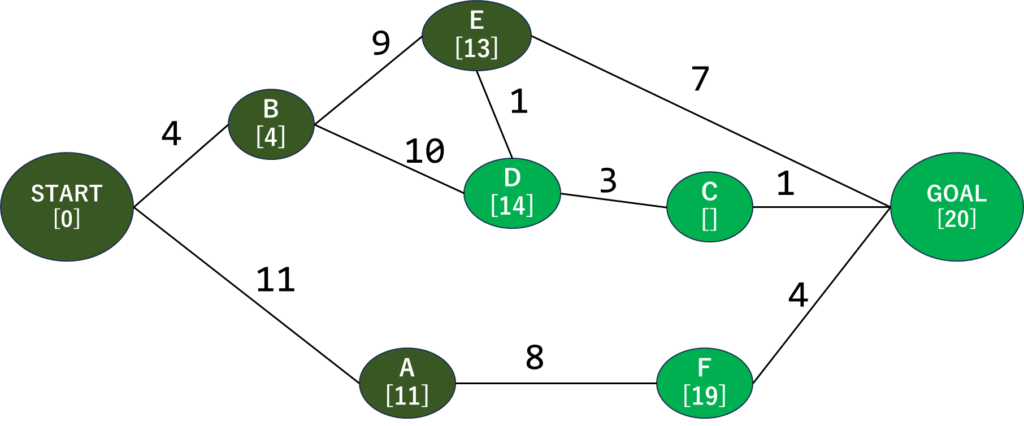
Eに隣接してる未探索の頂点はDとGOALですね。ここで、START⇒B⇒E⇒Dの経路がSTART⇒B⇒Dよりも短い場合はここで更新するんですが、たまたま同じ距離になってしまいました…テキトーに距離を割り振ったのがバレますね…うぅ
まぁ、ともかくまた最短の場所を確認しましょう。目的地に行けるようになりましたが、距離は20。どうやらDへ行く方が近そうです。Dに行きましょう。

さてDに来ました。隣接してる未探索ノードはCだけですね。距離を更新してジャンジャン行きましょう。
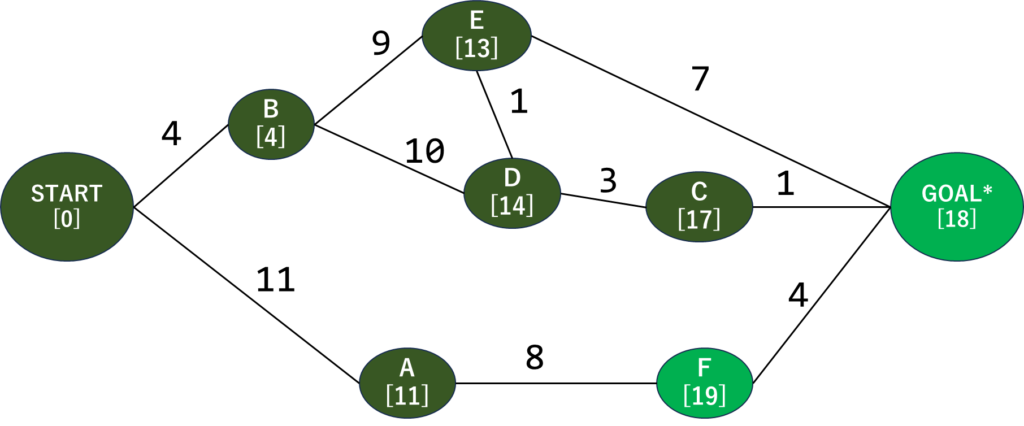
Cに来ました。Cの隣接ノードは…GOALだけですね。
さて、GOALに*を付けておきました。何があったかというと、START⇒B⇒E⇒GOALと行くときの距離の合計は確か20でしたね。しかし、E⇒D⇒Cと進むと距離の合計が18となって20より小さくなります。そのためGOALノードまでの最短距離を18で更新しました。ほら、WordとかPowerPointで更新してないと*でるじゃないですか…!あぁいう…ね!
さてラストスパートです。残った未探索ノードはGOALとFだけですね。GOALから先へは進めないのでいったんそのまま通り過ぎて、F行きましょう。
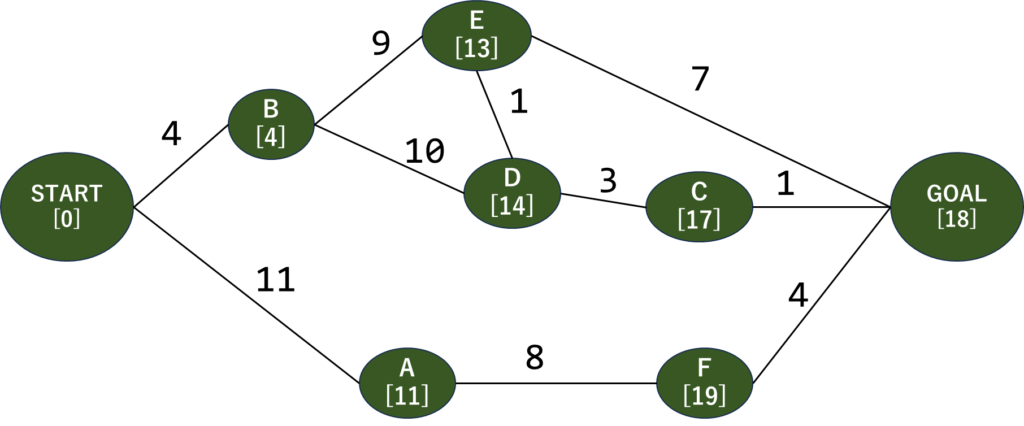
Fに来ました。Fから先に行くとGOALになりますが…距離の合計が23になって現在の最短距離である18より大きくなってしまいますね。なのでGOALの更新は入りません。
さて、グラフにあった全ノードの探索が終わりました!そしてGOALを見ると最短距離は「18」と記録されていますね。
そのため、このグラフにおける最短経路はSTART⇒B⇒D⇒C⇒GOALとなりますね。…まぁグラフの設計ミスってもう1個最短経路出てますがDの方が経由地少ないので今回はこっちを答えとしてみました。
実装編
さて、毎度のごとくGPT君に生成してもらい、動作を確認してみましょうか。ただ「ダイクストラ法で出して!」だけではなく、説明のためにちょっと修正を加えたりしてます。
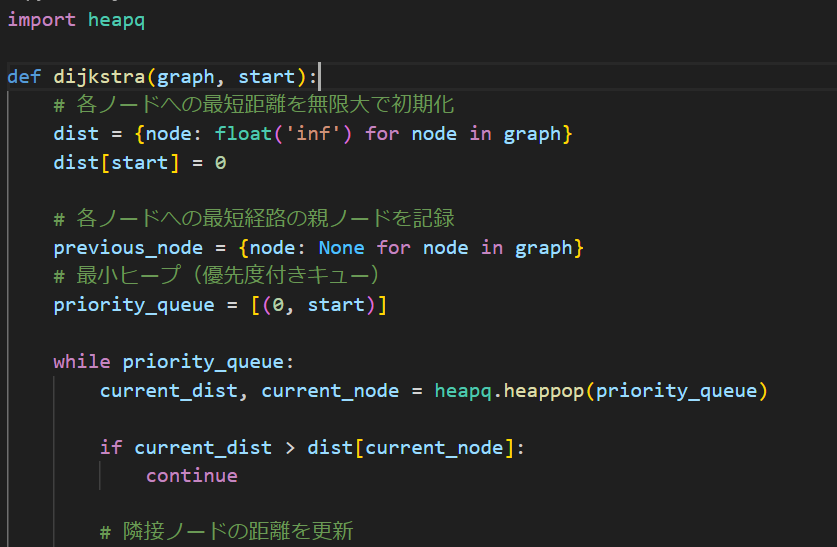

ちょっと長くなったので複数枚になりました。1枚ずつ行きましょう。あとこの段階で明言しておきますが、関数の中身だけでネストの説明とかは省きます。それと表示+確認用に生成してもらったところも省きます。字数がすごくなっちゃう…ごめん気になる人は調べて…!
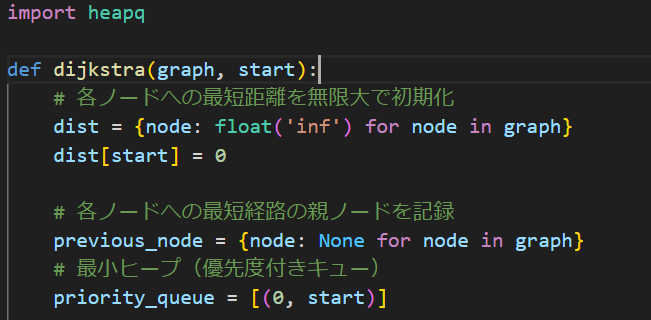
importしてるheapqは優先度付きキューなんて呼ばれるやつで、詳しくは省略しますがとにかく一番小さいものを取り出すデータ構造なんだなとだけ認識しておいてください。
まず関数の1行目で各ノードへの最短距離を無限大で初期化しておきます。こうすることで後で移動先を決めるときに誤作動するのを防ぎます。そしてSTARTを0にしておきます。
previous_nodeは表示+確認用で、priority_queueはデータを格納するheapキューです。この辺は宣言と初期化エリアですね。
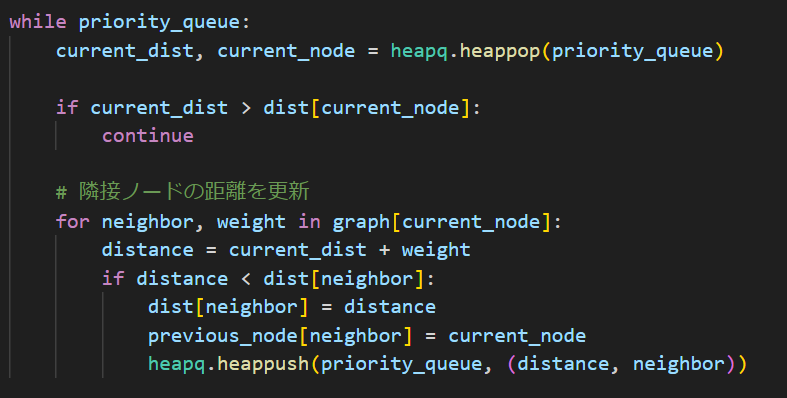
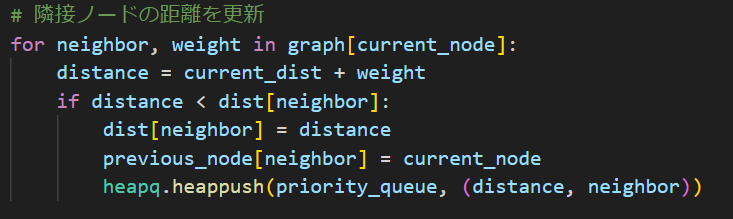
whileの中身です。heapq.heappopは一番小さいものを持ってくるやつです。
まず、current_dist(そこまでの距離)がdist[current_node]現時点での最短距離より大きかったら更新が発生しないので次に行きます。
そうじゃない場合は下のfor文に行きます。まずgraph(準備したグラフです)から接続してる近傍点(neighbor)と重み(基準点からそこへ行くまでの距離)を1つずつ取り出して、距離の比較・更新処理をここで行っています。heappushは要素追加するメソッドっていう認識でいいです。あとは割とそのままなので詳しくは割愛します。

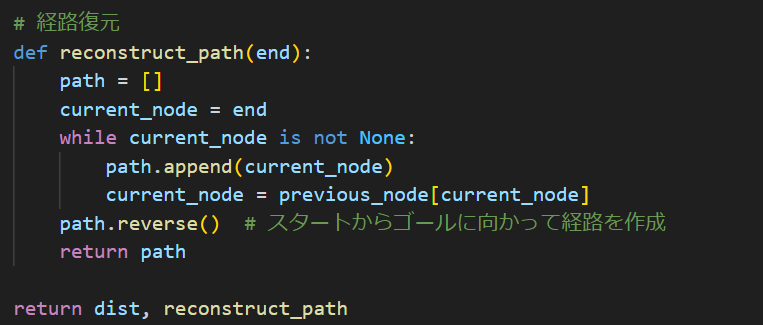
このreconstruct_path()はあとで経路の表示と確認をするために追加されたものです。これちゃんと説明するとネストされた関数についてで1チャプター書きそうなのでやめときます。ざっくりと言うと、たどれるように親ノードを紐づけてそれを逆算で戻って経路作成ができるようにしてます。

実行部分です。start_nodeで”START”を指定して、dijkstra関数を用いて最短経路を得ています。
下にあるのは結果表示のためのプログラムですね。やってることはいたって単純ですがまぁ詳しくはreconstruct_path()を確認してください。
こうしてみると案外仕組みはシンプルなアルゴリズムなんだなということがわかりますね。ちなみにダイクストラ法では重みが負・マイナスのものが扱えません。理由はまぁそういうものだからと言ったらおしまいですが…要はアルゴリズムの仕組み上、最短経路が確定した場所はもう見ないようにしてるんですがマイナスだと見る必要が生まれる場合があって…またこの辺りは機会があったら書きます。次行きましょう。
A*アルゴリズム
A*(エースター)アルゴリズムです。歴代で一番うまく説明できる自信がないです。やばい。どういう順で説明すればいいんだろうと思ってるんですが頑張ります。
A*アルゴリズムは言ってしまえばダイクストラ法の拡張版です。ダイクストラ法では結構網羅的に見ていったんですが、ここにヒューリスティック関数という概念…というか要素を追加します。
これを追加することによって探索範囲を減らして、より効率的に探索を進めるようにしたアルゴリズムになります。
まぁやっぱり図があった方がいいですね、準備しましょう。今回はこれまで見たいな木構造じゃなくて迷路的なものを用意します。その方が説明できそうなので…

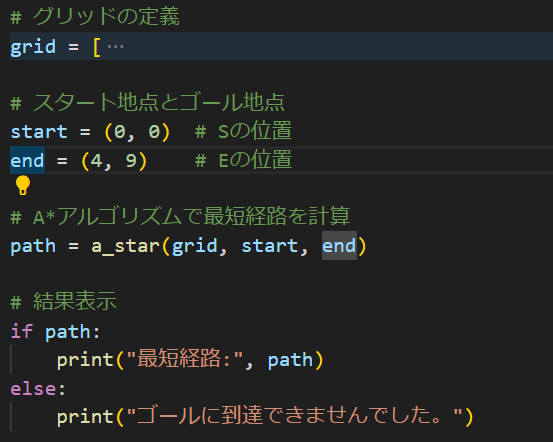
さて、こんな感じのものを用意したしました。後々出すプログラムから拝借したものです。SがSTARTでEがEND、まぁゴールですね。でOがObjectつまり障害物です。
この迷路でSTARTからENDに行くための最短経路を求めることを考えます。ここで最初に説明したものをもう少し細分化…というか掘り下げていきましょう。
ノードnにおけるゴールまでの総移動距離というか、評価値をF(n)と置きます。数学苦手な人逃げないでね。そしてスタート地点から現在の探索地点までの総距離をG(n)、ヒューリスティック関数をH(n)と置きます。この時、
F(n) = G(n) + H(n)
となります。
ヒューリスティック関数って何やねんって感じだと思うので説明します。ヒューリスティック自体の意味合いは確か「経験的に得られた知識」みたいなものだったと思いますが、ここでのヒューリスティック関数は、「現在の位置からゴールまでかかるであろうおおよその距離」を指します。
このヒューリスティック関数によって「今の地点からだと大体どれくらいかかるか」という視点が入るので探索効率を上げられるわけです。

ヒューリスティック関数は今回はマンハッタン距離という、そこに行くまでの縦の距離と横の距離(直線距離)を足し合わせたものを使います。例えば今青の★マークが探索箇所だとすると、緑矢印がマンハッタン距離、今回使用するヒューリスティック関数で、そこから上下左右に移動しながら最短経路を探しに行くわけです。
…うーん説明できているんでしょうか。ちょっと今回はプログラムを早めに出してそれも含めて確認していきましょう。(あと現時点で文字数が…)
実装編
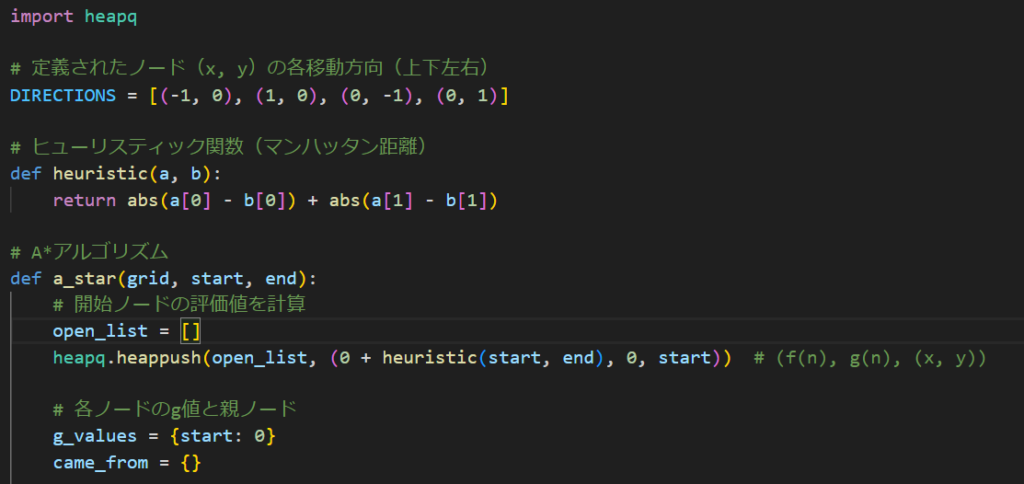
こんな感じですね。定義部分とか呼び出す部分は割とそのままなので説明割愛します。A*アルゴリズムの中身を確認しましょう。
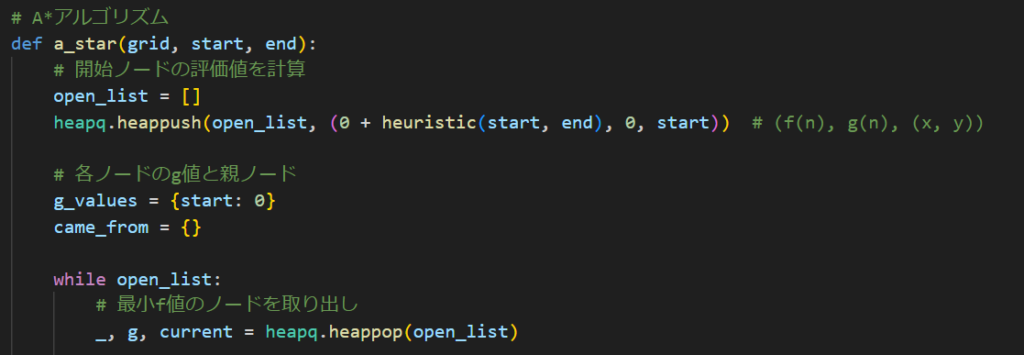
定義部分割愛すると言いましたが、A*アルゴリズムの序盤の定義だけ触れましょう。このopen_listってやつが探索する箇所のリストみたいなやつです。そして実装を楽にするために今回もheapqを使ってます。
g_valueにおけるG値って言うのがさっき触れたG(n)ですね。STARTから今探索している地点までの総移動距離になります。STARTはまぁSTARTなので当然0ですね。そして後ほど経路復元をするためにcame_fromというリストを用意してます。
こういった前提を基に本処理へ入ります。
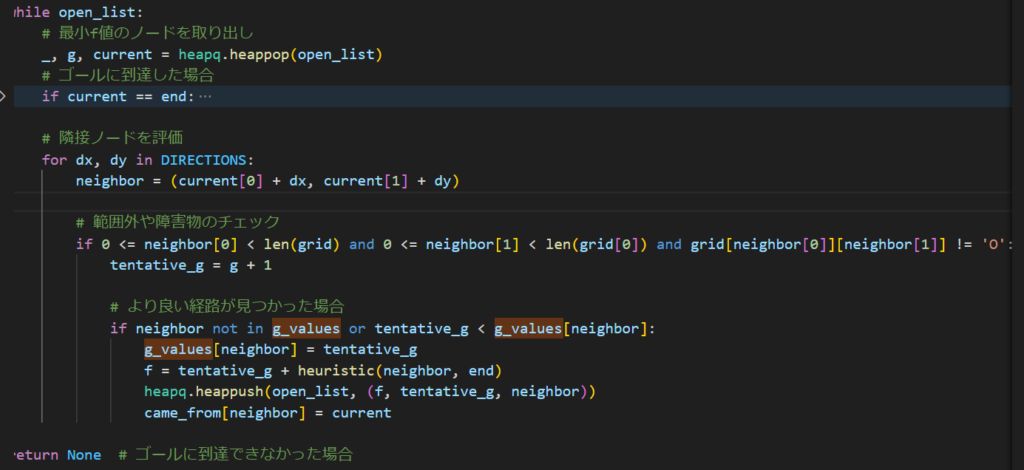
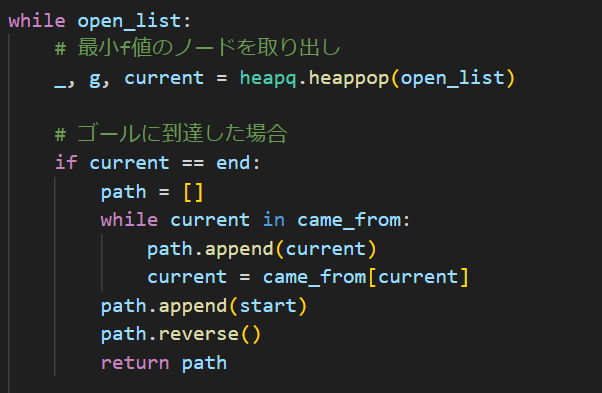
まずheappop()で、open_listからF値が最小値のものを1個取り出してきて、その中のG値と探索ノードを取り出します。
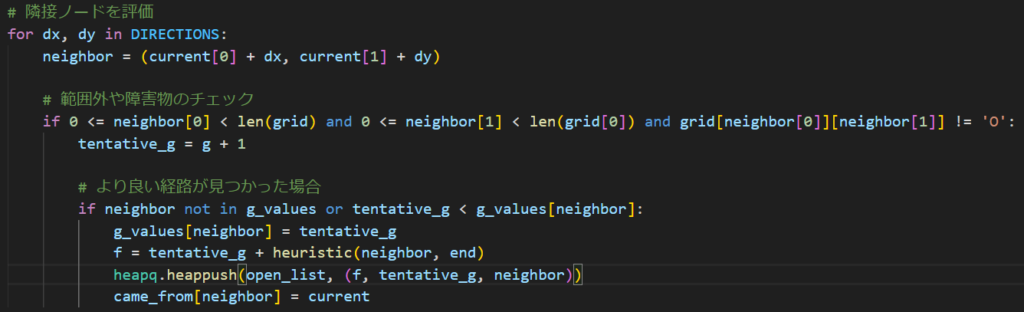
そして探索ノードの上下左右を確認するために、DIRECTIONSから順番に上下左右への移動量を取り出してます。それが

この部分ですね。ここで周辺(±1)の座標をneighborとして取り出して、そのneighborが「グリッド(迷路全体)の外に行かないか」「障害物とぶつからないか」を確認して、そうじゃない場合(=移動先がちゃんと通路)であれば、経路更新をするかどうかの確認に入ります。

経路更新部分です。隣接座標にあたるneighborがg_valueにまだない(=まだ登録されてない)かよりよい経路が見つかったとき、その時点でのG値とヒューリスティック値を足し合わせて登録、そして親ノードをcame_fromに登録していきます。
こんな感じで、STARTから移動可能な場所を移動しながら登録していって、登録されたリストからF値(G値+ヒューリスティック値)の一番小さいものを取り出して移動、周囲の移動可能な場所をF値を計算しながら登録、そしてまたF値の一番小さいものを…と繰り返してGOALを目指していくわけです。

そしてゴールについたときの処理がこれになります。やってることは単純で、今回経路を移動するときに移動するときの基準というか親ノードをcame_fromに記録してるので、それをpathというリストにendからstartまで登録していって、それをreverseメソッドで逆転させることでSTARTからENDまでの道順を再現してます。
これでA*アルゴリズムを実装しているわけです。こうしてプログラム的に考えると結構わかりやすい…ような?

実際に実行するとこうなります。
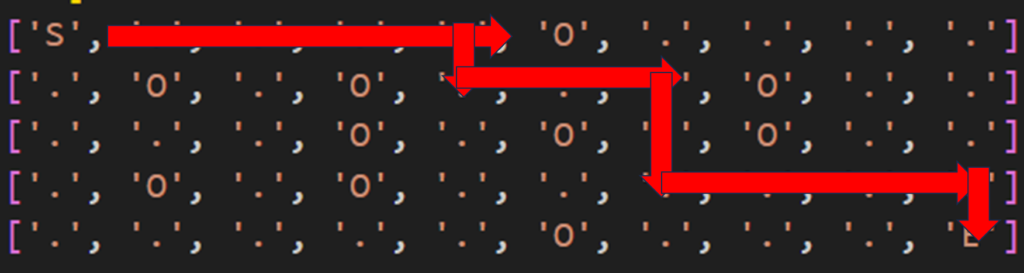
間違えてなければ多分こういった経路になってます。ぱっと見行けてそうですね。
以上、A*アルゴリズムでした。だいぶ試行錯誤と勉強をしながら書いてたのでごちゃごちゃしてたり間違ってたりしたら申し訳ないです。
終わりに
書きすぎた!!!!
短期集中連載って銘打ってサクッと終わらせるつもりで書き始めたはずなのに12000字書く馬鹿がどこにいるんでしょうkええはい私ですここ居ますマジで書きすぎましたでもあんまり後悔s
…はい。BFSとDFSだけのつもりが意地でダイクストラ法とA*アルゴリズムまで頑張っちゃいました。想定の数倍時間かかりましたが、まぁいい機会だったということで飲み込みます。
また間違いが無いか確認したり、文字装飾やコードブロック化などで見やすいように変更するつもりですが、いったん休憩させてください…最後ちょっと雑になった気がしますすいません。
短期集中連載は一応これで終わる予定です。3回分お付き合いいただきありがとうございました。自分としてもやったことないチャレンジだったのでどうなるかわかんなかったですがやり切れてよかったです。
それでは、ここまでライターはSyncorでした。また機会があればお会いいたしましょう。ばいば~い