第2回はこちら:ヒープソートと計算量
第3回はこちら:探索アルゴリズム
あいさつ
こんにちは、Syncor(シンクラー)です。毎回名前にルビを振るかどうか悩んでます。
この記事が年明け後初のものになるんでしょうか。これを書いている時点では不明ですがまぁとりあえず…
あけましておめでとうございます!
2025年もGSDと本ホームページをよろしくお願いいたします。こう書くことでうっすらと後輩たちに記事更新してねという圧をかけておくことにします。
前置きはさておき、個人的に最近「アルゴリズムちゃんと勉強しなおすべきだなぁ」と感じることが多く、知識としてうっすらどういったものかは理解しているつもりなのですが、ぱっと「説明して?」と言われるとちょっと自信ないなと…そんなわけで、色々調べながら改めてまとめなおして、勉強してみようと思い立ったわけです。まぁようはアウトプットです、アウトプット。本当は1本1本ゲーム作ってみればよかったかもですが本質を外れそうなので…ちょっとコード例を作ってみるぐらいは頑張ります。
そんな温度感です。全何回かは決めてないですが、短期集中連載のつもりです。生暖かく見ていただければ幸いです。それでは。
ソーティングするぞ!
さて、第1回はソーティングアルゴリズムについてです。探索アルゴリズムとかだとかなりしゃべれそうですが、ソーティングはそこまでかける自信ないので色々なものをざっくりまとめて書こうと思います。
あと頑張れる範囲でですが、実行例も作ろうかと思います。環境組む楽さとシンプルさからVisual Studio CodeとPythonで作ります。また、ソーティングする対象は配列ということにします。間違ってたら許してくださいなんでもはしません。あ、あとChatGPTの力も借ります。
バブルソート
まずはバブルソート(Bubble Sort)から行きましょう。バブルソートは配列内要素の隣接した要素同士を比較して、どんどんずらしながら整理するソーティング方法、ですかね。
例えば、ランダムに数値が入った数列があるとしましょう。そしてこれを小さい順に並べなおそうとすると。とりあえずなんとなくで作ってみましょうか。

まず0番目と1番目を見ると、1と5で1番目の方が大きいですね。今回は小さい順にするのでそのままにしましょう。
では次に1番目と2番目を見比べましょう。すると5と3で今度は2番目の方が小さいことがわかります。なので今回は入れ替えます。そうすると、[1,3,5,9,7,4,2]となります。
同様に2番目と3番目を比較します。今回は9の方が大きいのでそのまま、3番目と4番目を見ると7の方が小さいので入れ替え…と進めていき、1巡すると

こうなると思います。見ていただければわかると思いますが、これ整理されているように見えてまだですね。まだまだやる必要がありそうです。
バブルソートは処理をグルグルと繰り返すわけです。一番端っこは整理済みになるので、その分はやらなくて済むのですが…まぁそのため処理時間は結構かかります。今回は概要重視で比較するわけではないのでランダウの記号関係は省略しますが…
あ、これ以降もコード画像+コードブロックの並びにします。コードブロックのみだとちょっと見づらそうなので…
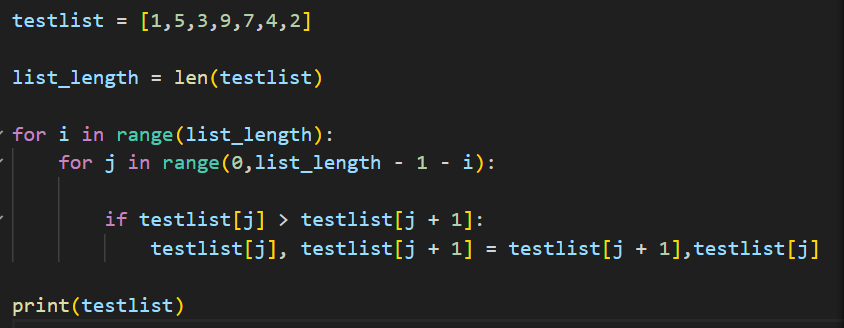
testlist = [1,5,3,9,7,4,2]
list_length = len(testlist)
for i in range(list_length):
for j in range(0,list_length - 1 - i):
if testlist[j] > testlist[j + 1]:
testlist[j], testlist[j + 1] = testlist[j + 1],testlist[j]
print(testlist)サクッと書いてみました。こんな感じですかねぇ。
超シンプルなアルゴリズムという感じです。その分実装も楽ですし、小さいものにやる分には使えそうです。
クイックソート
さて、ではクイックソート(Quick Sort)に行きましょう。アルゴリズムは早いに越したことはないですからね。
クイックソートは、代表値を1個決めてそれより大きい部分と小さい部分に分ける、という処理を再帰的に何度も何度も繰り返して整理していくアルゴリズム…で説明できてるんですかね。あんまり自信ないです。
とりあえず新しい配列用意しましょうか。

ではまず代表値、ピポットとか基準値の方がいいでしょうか。まぁ呼び方は何でもいいですがとりあえず…末尾の9にしましょうか。(真ん中は1にしちゃったので…)
まず9より小さい要素と大きい要素で分けましょう。そうすると、
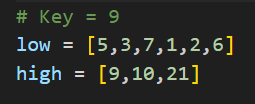
こうなりますかね。9はhighの方に入れちゃいました。数少なかったし。
ここでlow配列とhigh配列を比べると、high配列に入ってる要素は全てlow配列の要素よりも大きくなってることがわかりますね。この性質を利用して整理していくわけです。バブルソートよりも早く終わりそうな感じがしますね。
同じ感じでlow配列を整理してみましょう。本当は分けた配列どっちもやらなきゃなんですが、たまたまhigh配列が整理されてたので省略します。(本当のマジのガチでたまたまです信じてください)
先ほどと同じように代表値は末尾の6にしましょう。整理すると
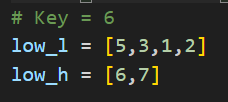
こうですね。こんな感じで整理していくわけです。ちょっと全部やると書くのが大変なのでここで省略しますが、これを繰り返していくわけです。計算オーダーはバブルソートに比べてだいぶ小さくなりそうですね。
ではサンプルコードを作ってみましょうか。ここでは再帰呼び出しという方法?テクニック?を使います。詳しい説明は省きます。関数の中で関数呼ぶみたいなあれです。
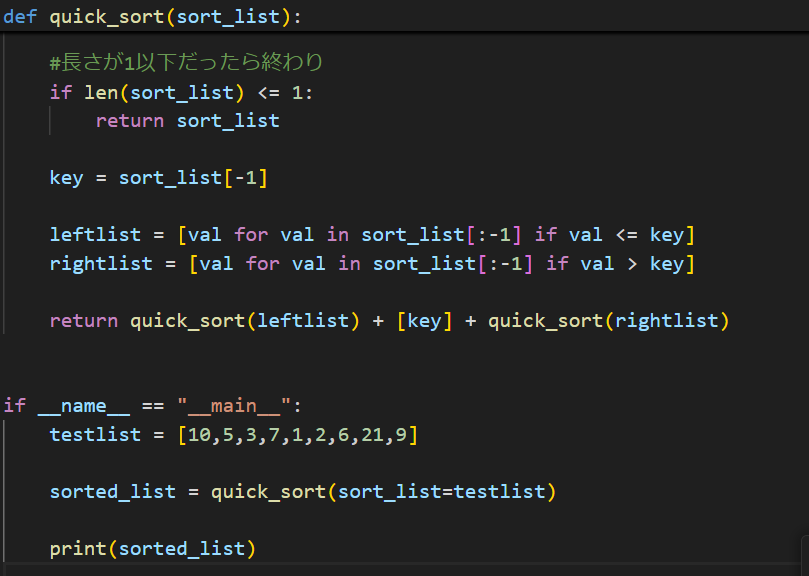
def quick_sort(sort_list):
#長さが1以下だったら終わり
if len(sort_list) <= 1:
return sort_list
key = sort_list[-1]
leftlist = [val for val in sort_list[:-1] if val <= key]
rightlist = [val for val in sort_list[:-1] if val > key]
return quick_sort(leftlist) + [key] + quick_sort(rightlist)
if __name__ == "__main__":
testlist = [10,5,3,7,1,2,6,21,9]
sorted_list = quick_sort(sort_list=testlist)
print(sorted_list)
さて、こんな感じですかね。なんとかうまく動いてるようにも見えます。
余談ですが、pythonの配列内でifとかfor書くやつ、リスト内包表記…でしたっけ?あれ便利ですよねぇ…python以外であんま見ない気がするんですが、演算子のオーバーロードだとか駆使したら多言語でもできたりするんでしょうか。暇なときに調べてみようと思います。
マージソート
さて、最後にマージソート(Merge Sort)に触れましょう。バブルソートとクイックソートだけにしようかと思いましたが、2つだけだとなんか寂しいですし、大事なものだと思うので…
マージソートはその名の通り、対象とする配列を分割して整理してその後合体、マージするといった手法のソーティングアルゴリズムです。…合ってるよね?
ではまず、毎度のごとく配列を用意しましょう。

こんな感じですかね。ではまず分けましょうか。クイックソートみたく大小関係なしに割ります。

配列の名前テキトーじゃんってツッコミは無しです。たまたま偶数個だったので綺麗に分割できました。まだまだ行きましょう。
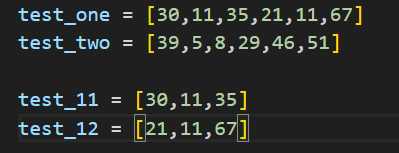
さらに半分になりましたね。この分割作業を、それぞれが要素1個の配列になるまでやります。
すると、[30],[11]となりますね。では分割しきったところで今度はマージです。この2つを比較すると11の方が明らかに小さいですよね?なので、並び替えてマージすると、[11,30]という配列ができます。今度はこれとさっき余った[35]を比べて、また並び替えると[11,30,35]となりますね。
これをそれぞれの要素に行っていきます。分割が終わった時点で全12個の配列ができていたので、これをどんどんマージしていくわけです。
…ちょっと自信ないですけどちゃんと説明できてますかね?


def merge_sort(arr):
#リストの長さが1以下の場合はそのまま返す
if len(arr) <= 1:
return arr
#リストを2つに分割
mid = len(arr) // 2
left = arr[:mid]
right = arr[mid:]
# 左右のリストを再帰的にソート
left_sorted = merge_sort(left)
right_sorted = merge_sort(right)
# ソートされたリストをマージして返す
return merge(left_sorted, right_sorted)
def merge(left, right):
sorted_list = []
i = j = 0
# 左右のリストを比較しながら順番にマージ
while i < len(left) and j < len(right):
if left[i] < right[j]:
sorted_list.append(left[i])
i += 1
else:
sorted_list.append(right[j])
j += 1
# 残った要素を追加
sorted_list.extend(left[i:])
sorted_list.extend(right[j:])
return sorted_list
if __name__ == "__main__":
# サンプルリスト
testlist = [30,11,35,21,11,67,39,5,8,29,46,51]
# ソート前のリスト
print("ソート前:", testlist)
# マージソートを実行
sorted_arr = merge_sort(testlist)
# ソート後のリスト
print("ソート後:", sorted_arr)サンプルコードはこんな感じ…というかGPT君に作ってもらいました。こういう時本当に便利ですね。ここでも再帰呼び出しが使われています。こういったアルゴリズムの話をするときにはつきものですね。
終わりに
さて、いかがでしたでしょうか。弊サークルあんまこういう記事ない気がするので、ちょっとチャレンジしてみました。ずいぶんゆる~く長々と書いてしまったように感じますが、何かしらの参考等になっていましたら幸いです。
次の内容ですが、実はこの短期集中連載、全3回の予定だったんですが2回分しかネタを用意できず…どうしようかと考えていたんですが、この記事を書いてるときにあんまり耳馴染みがなかったものがあったこと、それから今回割愛した計算時間の話はやっぱすべきかと感じたのでその話、つまり今回書かなかったものを書く会、言ってしまえば後編にしようかなと考えてます。今回みたくゆる書く予定ですが、もしよければ覗いて行ってください。
それでは、Syncorでした~また次回~